题目内容
19.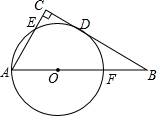 如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.
如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形.
(2)若AC=6,AB=10,连结AD,求⊙O的半径和AD的长.
分析 (1)连接OD、OE、ED.先证明△AOE是等边三角形,得到AE=AO=0D,则四边形AODE是平行四边形,然后由OA=OD证明四边形AODE是菱形;
(2)连接OD、DF.先由△OBD∽△ABC,求出⊙O的半径,然后证明△ADC∽△AFD,得出AD2=AC•AF,进而求出AD.
解答 (1)证明:如图1,连接OD、OE、ED.
∵BC与⊙O相切于一点D,
∴OD⊥BC,
∴∠ODB=90°=∠C,
∴OD∥AC,
∵∠B=30°,
∴∠A=60°,
∵OA=OE,
∴△AOE是等边三角形,
∴AE=AO=0D,
∴四边形AODE是平行四边形,
∵OA=OD,
∴四边形AODE是菱形.
(2)解:设⊙O的半径为r.
∵OD∥AC,
∴△OBD∽△ABC.
∴$\frac{OD}{AC}=\frac{OB}{AB}$,即10r=6(10-r).
解得r=$\frac{15}{4}$,
∴⊙O的半径为$\frac{15}{4}$.
如图2,连接OD、DF.
∵OD∥AC,
∴∠DAC=∠ADO,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠DAC=∠DAO,
∵AF是⊙O的直径,
∴∠ADF=90°=∠C,
∴△ADC∽△AFD,
∴$\frac{AD}{AC}=\frac{AF}{AD}$,
∴AD2=AC•AF,
∵AC=6,AF=$\frac{15}{4}×2=\frac{15}{2}$,
∴AD2=$\frac{15}{2}$×6=45,
∴AD=$\sqrt{45}$=3$\sqrt{5}$.
点评 本题考查了切线的性质、圆周角定理、等边三角形的判定与性质、菱形的判定和性质以及相似三角形的判定和性质,是一个综合题,难度中等.熟练掌握相关图形的性质及判定是解本题的关键.

练习册系列答案
相关题目
4.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
| A. | 60° | B. | 72° | C. | 90° | D. | 108° |
10.今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.

请结合统计图表,回答下列问题.
(1)统计表中m=15%,图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(2)请补全图1示数的条形统计图;
(3)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.

| 对雾霾了解程度的统计表 | |
| 对雾霾的了解程度 | 百分比 |
| A.非常了解 | 5% |
| B.比较了解 | M |
| C.基本了解 | 45% |
| D.不了解 | N |
(1)统计表中m=15%,图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(2)请补全图1示数的条形统计图;
(3)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
11.下列各组线段中,能够组成直角三角形的一组是( )
| A. | 1,2,3 | B. | 2,3,4 | C. | 4,5,6 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
9. 如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是( )
如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是( )
 如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是( )
如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是( )| A. | πcm2 | B. | 2πcm2 | C. | 4πcm2 | D. | 8πcm2 |
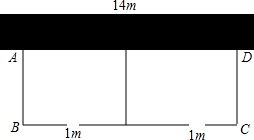 如图,要建一个长方形养鸡场(分为两片),养鸡场的一边靠着一面长14m的墙,另几条边及中间隔开的边用总长22m的竹篱围成,每片养鸡场的前面各开一扇宽为1m的门,门用其他材料另外制作,如果要围成总面积为45m2的养鸡场,设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{24-3x}$,根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,x=5满足你所列的方程并符合题意吗?x=3呢?请说明理由.
如图,要建一个长方形养鸡场(分为两片),养鸡场的一边靠着一面长14m的墙,另几条边及中间隔开的边用总长22m的竹篱围成,每片养鸡场的前面各开一扇宽为1m的门,门用其他材料另外制作,如果要围成总面积为45m2的养鸡场,设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{24-3x}$,根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,x=5满足你所列的方程并符合题意吗?x=3呢?请说明理由. 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是92%.
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是92%. 如图所示是由8个相同的小正方体组成的一个几何体,则这个几何体的主视图是( )
如图所示是由8个相同的小正方体组成的一个几何体,则这个几何体的主视图是( )



 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是$\frac{3}{4}$.