题目内容
16. 如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是4.
如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是4.
分析 首先根据CD平分∠ACB交AB于点D,可得∠DCE=∠DCF;再根据DE⊥AC,DF⊥BC,可得∠DEC=∠DFC=90°,然后根据全等三角形的判定方法,判断出△CED≌△CFD,即可判断出DF=DE;最后根据三角形的面积=底×高÷2,求出△BCD的面积是多少即可.
解答 解:∵CD平分∠ACB交AB于点D,
∴∠DCE=∠DCF,
∵DE⊥AC,DF⊥BC,
∴∠DEC=∠DFC=90°,
在△DEC和△DFC中,
$\left\{\begin{array}{l}{∠DCE=∠DCF}\\{∠DEC=∠DFC}\\{CD=CD}\end{array}\right.$(AAS)
∴△DEC≌△DFC,
∴DF=DE=2,
∴S△BCD=BC×DF÷2
=4×2÷2
=4
答:△BCD的面积是4.
故答案为:4.
点评 (1)此题主要考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:角的平分线上的点到角的两边的距离相等.
(2)此题还考查了全等三角形的判定和性质的应用,以及三角形的面积的求法,要熟练掌握.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
11.下列各组线段中,能够组成直角三角形的一组是( )
| A. | 1,2,3 | B. | 2,3,4 | C. | 4,5,6 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为3.
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为3.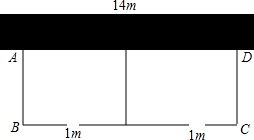 如图,要建一个长方形养鸡场(分为两片),养鸡场的一边靠着一面长14m的墙,另几条边及中间隔开的边用总长22m的竹篱围成,每片养鸡场的前面各开一扇宽为1m的门,门用其他材料另外制作,如果要围成总面积为45m2的养鸡场,设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{24-3x}$,根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,x=5满足你所列的方程并符合题意吗?x=3呢?请说明理由.
如图,要建一个长方形养鸡场(分为两片),养鸡场的一边靠着一面长14m的墙,另几条边及中间隔开的边用总长22m的竹篱围成,每片养鸡场的前面各开一扇宽为1m的门,门用其他材料另外制作,如果要围成总面积为45m2的养鸡场,设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{24-3x}$,根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,x=5满足你所列的方程并符合题意吗?x=3呢?请说明理由. 如图所示是由8个相同的小正方体组成的一个几何体,则这个几何体的主视图是( )
如图所示是由8个相同的小正方体组成的一个几何体,则这个几何体的主视图是( )



 过点(0,-2)的直线l1:y1=kx+b(k≠0)与直线l2:y2=x+1交于点P(2,m).
过点(0,-2)的直线l1:y1=kx+b(k≠0)与直线l2:y2=x+1交于点P(2,m). 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是$\frac{3}{4}$.