题目内容
14.解不等式组:$\left\{\begin{array}{l}{3(x+1)>x-1}\\{-\frac{2}{3}x+8≤2}\end{array}\right.$.分析 分别解出不等组中两不等式的解集,取其公共部分即可得出结论.
解答 解:解不等式3(x+1)>x-1,
得:x>-2;
解不等式-$\frac{2}{3}$x+8≤2,
得:x≥9.
故不等式组$\left\{\begin{array}{l}{3(x+1)>x-1}\\{-\frac{2}{3}x+8≤2}\end{array}\right.$的解为x≥9.
点评 本题考查了解一元一次不等式组,解题的关键是分别求出两不等式的解集取其交集.本题属于基础题,难度不大,解集该题型题目时,牢记解不等式组的方法及步骤是关键.

练习册系列答案
相关题目
6.下列调查中,最适合采用抽样调查的是( )
| A. | 乘坐高铁对旅客的行李的检查 | |
| B. | 了解全校师生对重庆一中85周年校庆文艺表演节目的满意程度 | |
| C. | 调查初2016级15班全体同学的身高情况 | |
| D. | 对新研发的新型战斗机的零部件进行检查 |
 ;
;
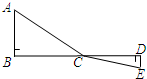 阅读材料:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为$\sqrt{16+(8-x)^{2}}$+$\sqrt{4+{x}^{2}}$.然后利用几何知识可知:当A、C、E在一条直线上时,x=$\frac{8}{3}$时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式$\sqrt{25+(12-x)^{2}}$+$\sqrt{9+{x}^{2}}$的最小值为4$\sqrt{13}$.
阅读材料:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为$\sqrt{16+(8-x)^{2}}$+$\sqrt{4+{x}^{2}}$.然后利用几何知识可知:当A、C、E在一条直线上时,x=$\frac{8}{3}$时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式$\sqrt{25+(12-x)^{2}}$+$\sqrt{9+{x}^{2}}$的最小值为4$\sqrt{13}$.