题目内容
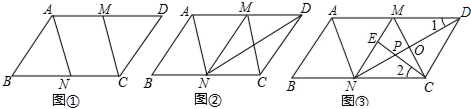
9.在?ABCD中,M,N分别是AD,BC的中点,连接AN,CM.(1)如图①,求证:四边形ANCM是平行四边形;
(2)如图②,连接MN,DN,若∠AND=90°,求证:MN=NC;
(3)如图③,在(2)的条件下,过点C作CE⊥MN于点E,交DN于点P,EP=1,且∠1=∠2,求AN的长.
分析 (1)由平行四边形ABCD,得到一组对边间关系,由中点可得到一组对边平行且相等,从而判定四边形ANCM是平行四边形;
(2)可利用直角三角形斜边的中线与斜边的关系,进行证明;
(3)先判定四边形MNCD是平行四边形,再判断其为菱形,利用菱形的性质,判断△MNC为等边三角形,从而求得∠1=∠2=∠MND=30°,在RT△NEP中,利用特殊角,求出EN,进而求出线段AN的长.
解答 解:(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵M,N分别是AD、BC的中点,
∴AM=CN,AM∥CN,
所以四边形ANCM是平行四边形;
(2)证明:∵∠AND=90°,AM=DM,
∴MN=$\frac{1}{2}$AD=MD,
∵MD=$\frac{1}{2}$AD=$\frac{1}{2}$BC=CN,
∴MN=NC;
(3)解:∵MD=$\frac{1}{2}$AD=$\frac{1}{2}$BC=CN,MD∥CN
∴四边形MNCD是平行四边形,
由(2)知MN=NC
∴?MNCD是菱形,
∴∠NMC=∠DMC,DN⊥MC,∠DNM=∠DNC,
∵∠1+∠DMC=∠1+∠NMC=∠2+∠ENC=90°,
∴∠NMC=∠MNC,
∴MN=CN=MC,
∴△MCN是等边三角形,
∴∠MND=∠2=∠1=30°,
在RT△NEP中,∵EP=1,
∴NE=$\sqrt{3}$,
所以MN=MC=2$\sqrt{3}$,
∵四边形AMCN是平行四边形,
∴AN=MC=2$\sqrt{3}$.
点评 本题是四边形的综合题,考察了平行四边形的性质和判定,菱形的判定与性质、直角三角形的斜边中线与斜边的关系、等边三角形的性质和判定以及相似三角形的性质和判定,利用直角三角形中30°的角所对的直角边与斜边的关系是求解的关键.

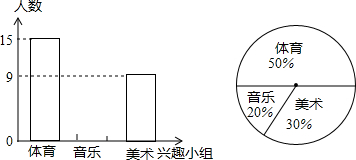
| A. | 八年级(1)班参加这三个课外兴趣小组的学生总人数为30人 | |
| B. | 在扇形统计图中,八年级(1)班参加音乐兴趣小组的学生人数所占的圆心角度数为82° | |
| C. | 八年级(1)班参加音乐兴趣小组的学生人数为6人 | |
| D. | 若该校八年级参加这三个兴趣小组的学生共有200人,那么估计全年级参加美术兴趣小组的学生约有60人 |