题目内容
4.居民区内的“广场舞”引起媒体关注,某都市频道媒体为此进行过专访报道,小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.

分析 (1)由A层次的人数除以所占的百分比求出调查的学生总数即可;
(2)由D层次人数除以总人数求出D所占的百分比,再求出B所占的百分比,再乘以总人数可得B层次人数,用总人数乘以C层次所占的百分比可得C层次的人数不全图形即可;
(3)用360°乘以C层次的人数所占的百分比即可得“C”层次所在扇形的圆心角的度数;
(4)求出样本中A层次与B层次的百分比之和,乘以4000即可得到结果.
解答 解:(1)90÷30%=300(人),
答:本次被抽查的居民有300人;
(2)D所占的百分比:30÷300=10%
B所占的百分比:1-20%-30%-10%=40%,
B对应的人数:300×40%=120(人),
C对应的人数:300×20%=60(人),
补全统计图,如图所示: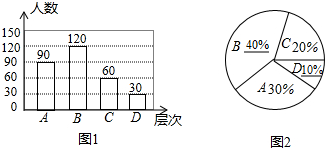
(3)360°×20%=72°,
答:“C”层次所在扇形的圆心角的度数为72°;
(4)4000×(30%+40%)=2800(人),
答:估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有2800人.
点评 此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.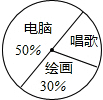 如图是八年级(2)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数为( )
如图是八年级(2)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数为( )
 如图是八年级(2)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数为( )
如图是八年级(2)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数为( )| A. | 36° | B. | 72° | C. | 108° | D. | 180° |
19.如图是某市某中学八年级(1)班学生参加音乐、美术、体育课外兴趣小组人数的部分条形统计图和扇形统计图,则下列说法错误的是( )
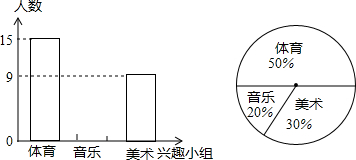

| A. | 八年级(1)班参加这三个课外兴趣小组的学生总人数为30人 | |
| B. | 在扇形统计图中,八年级(1)班参加音乐兴趣小组的学生人数所占的圆心角度数为82° | |
| C. | 八年级(1)班参加音乐兴趣小组的学生人数为6人 | |
| D. | 若该校八年级参加这三个兴趣小组的学生共有200人,那么估计全年级参加美术兴趣小组的学生约有60人 |
16.已知点P1(-4,3)和P2(-4,-3),则P1和P2( )
| A. | 关于原点对称 | B. | 关于y轴对称 | C. | 关于x轴对称 | D. | 不存在对称关系 |
14.如果把分式$\frac{xy}{x+y}$中的x和y都扩大为原来的2倍,那么分式的值( )
| A. | 扩大为原来的4倍 | B. | 扩大为原来的2倍 | C. | 不变 | D. | 缩小为原来的$\frac{1}{2}$ |

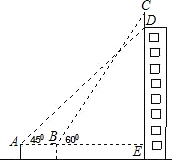 如图某幢大楼顶部有一广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一直线(∠AEC=90°)上,若BE=15米,求这块广告牌的CD.(取 $\sqrt{3}$=1.73,计算结果保留整数)
如图某幢大楼顶部有一广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一直线(∠AEC=90°)上,若BE=15米,求这块广告牌的CD.(取 $\sqrt{3}$=1.73,计算结果保留整数)