题目内容
19.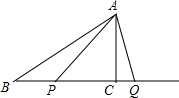 如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=acm,动点P,Q分别从点B,点C开始沿着射线BC运动,点P的速度为2cm/s,点Q的速度为1cm/s.两点同时出发,当点P追上点Q时两点都停止运动,设运动时间为t秒.
如图,Rt△ABC中,∠ACB=90°,BC=4cm,AC=acm,动点P,Q分别从点B,点C开始沿着射线BC运动,点P的速度为2cm/s,点Q的速度为1cm/s.两点同时出发,当点P追上点Q时两点都停止运动,设运动时间为t秒.(1)若a=2cm
①求两点都停止运动时,△ABQ的面积.
②是否存在t,使得△APQ为等腰三角形?若存在,请求出t的值;若不存在,请说明理由;
(2)若刚好存在某一时刻t,使得AP,AC三等分∠BAQ,则a的值为$\frac{2\sqrt{3}}{3}$(直接写出答案).
分析 (1)①根据“BP=BC+CQ”列出关于t的方程并解答即可;
②需要分类讨论:以AP为腰和以AP为底两种情况进行讨论;
(2)当AP,AC三等分∠BAQ时,AP平分∠BAC,结合角平分线定理来求a的值.
解答 解:(1)依题意得:2t-4=t,
解得t=4.
∴S△ABQ=$\frac{1}{2}$BQ•AC=$\frac{1}{2}$×8×2=8;
(2)①当PA=PQ时,$\sqrt{(4-2t)^{2}+{2}^{2}}$=4-2t+t,
解得t1=$\frac{2}{3}$,t2=2.
②当AP=AQ时,4-2t=t,
解得t=$\frac{4}{3}$;
③当AQ=QP时,$\sqrt{{t}^{2}+{2}^{2}}$=4-2t+t,
解得t=$\frac{3}{2}$.
综上所述,符合条件的t的值为:$\frac{2}{3}$或2或$\frac{4}{3}$或$\frac{3}{2}$.
(3)∵AP,AC三等分∠BAQ,
∴AP平分∠BAC,
∴$\frac{BP}{CP}$=$\frac{AB}{AC}$,即$\frac{2×\frac{4}{3}}{4-2×\frac{4}{3}}$=$\frac{\sqrt{{a}^{2}+{2}^{2}}}{a}$,
整理,得
a2+4=4a2,
解得a=$\frac{2\sqrt{3}}{3}$.
故答案是:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了等腰三角形的性质.解答(2)题时,没有明确指出等腰三角形的顶点,需要分类讨论,以防漏解或错解.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
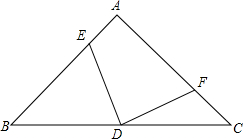 如图,已知等腰直角三角形△ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF.求证:DE=DF;DE⊥DF.
如图,已知等腰直角三角形△ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF.求证:DE=DF;DE⊥DF.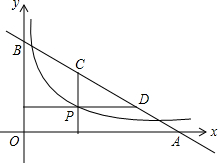 如图,P是函数y=$\frac{\sqrt{3}}{x}$(x>0)图象上的一点,直线y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与x轴、y轴别交于A,B两点,过P作x轴、y轴的垂线与该直线分别交于C,D两点,则AD•BC=4.
如图,P是函数y=$\frac{\sqrt{3}}{x}$(x>0)图象上的一点,直线y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与x轴、y轴别交于A,B两点,过P作x轴、y轴的垂线与该直线分别交于C,D两点,则AD•BC=4.