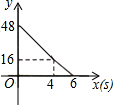题目内容
15.人造地球卫星要绕地球旋转,必须克服地球引力,克服地球引力的速度称为逃逸速度,逃逸速度的计算公式为$v=\sqrt{gR}$(千米/秒),其中g=0.0098千米/秒2,R=6370千米,求逃逸速度.(结果保留2个有效数字)分析 首先将g和R的值代入,然后再依据算术平方根的定义求解、最后在保留2个有效数字即可.
解答 解:$v=\sqrt{gR}$=$\sqrt{0.0098×6370}$=$\sqrt{62.426}$≈7.9千米/秒.
答:逃逸速度为7.9千米/秒.
点评 本题主要考查的是算术平方根的应用,将g、R的值代入,然后求得$\sqrt{gR}$的值是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
6.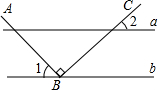 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 125° |
3.为确保信息安全,信息需加密传输,发送方由明文→密文(加密);接收方由密文→明文(解密).已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d.例如:明文1,2,3,4对应的密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
| A. | 4,6,1,7 | B. | 4,1,6,7 | C. | 6,4,1,7 | D. | 1,6,4,7 |
10.一个直角三角形中,两条直角边长为3和4,则它的斜边长为( )
| A. | 2 | B. | $\sqrt{7}$ | C. | 5 | D. | 25 |
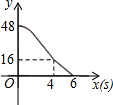
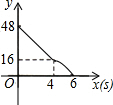
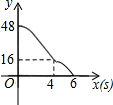
5.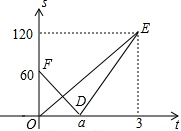 甲、乙两辆遥控车沿直线AC作同方向的匀速运动,甲、乙同时分别从A、B出发,沿轨道到达C处,已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处距离分别为S1,S2,函数关系如图所示,当两车的距离小于10米时,信号会产生相互干扰,那么t是下列哪个值时两车的信号会相互干扰( )
甲、乙两辆遥控车沿直线AC作同方向的匀速运动,甲、乙同时分别从A、B出发,沿轨道到达C处,已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处距离分别为S1,S2,函数关系如图所示,当两车的距离小于10米时,信号会产生相互干扰,那么t是下列哪个值时两车的信号会相互干扰( )
 甲、乙两辆遥控车沿直线AC作同方向的匀速运动,甲、乙同时分别从A、B出发,沿轨道到达C处,已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处距离分别为S1,S2,函数关系如图所示,当两车的距离小于10米时,信号会产生相互干扰,那么t是下列哪个值时两车的信号会相互干扰( )
甲、乙两辆遥控车沿直线AC作同方向的匀速运动,甲、乙同时分别从A、B出发,沿轨道到达C处,已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处距离分别为S1,S2,函数关系如图所示,当两车的距离小于10米时,信号会产生相互干扰,那么t是下列哪个值时两车的信号会相互干扰( )| A. | $\frac{2}{3}$ | B. | 2 | C. | $\frac{11}{5}$ | D. | $\frac{13}{5}$ |
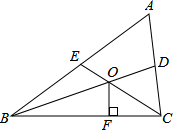 如图,△ABC 的中线BD、CE相交于点O,OF⊥BC,且AB=6,BC=5,AC=4,OF=3,则四边形ADOE的面积是7.5.
如图,△ABC 的中线BD、CE相交于点O,OF⊥BC,且AB=6,BC=5,AC=4,OF=3,则四边形ADOE的面积是7.5.
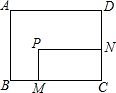 如图,矩形ABCD,AB=6,AD=8;动点M、N从点C出发,分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动,分别至点B、点D停止.作矩形PMCN.若运动时间为x(单位:s),设矩形ABCD除去矩形PMCN后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )
如图,矩形ABCD,AB=6,AD=8;动点M、N从点C出发,分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动,分别至点B、点D停止.作矩形PMCN.若运动时间为x(单位:s),设矩形ABCD除去矩形PMCN后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )