题目内容
10.(1)(2a+1)2-(2a+1)(-1+2a)(2)$\frac{1}{2}$a2bc3•(-2a2b2c)2
(3)(2x-y)(4x2-y2)(2x+y)
(4)(54x2y-108xy2-36xy)÷18xy
(5)(2x+3y)(2x-3y)-(2x+3y)2.
分析 (1)根据完全平方公式和平方差公式将原式展开,再合并同类项即可解答本题;
(2)根据积的乘方和同底数幂的乘法进行计算即可解答本题;
(3)根据乘法的结合律,利用平方差公式和完全平方公式可以对原始化简;
(4)根据多项式除以单项式的方法进行计算即可解答本题;
(5).根据平方差公式和完全平方公式将原式展开,再合并同类项即可解答本题.
解答 解:(1)(2a+1)2-(2a+1)(-1+2a)
=4a2+4a+1-(4a2-1)
=4a2+4a+1-4a2+1
=4a+2;
(2)$\frac{1}{2}$a2bc3•(-2a2b2c)2
=$\frac{1}{2}{a}^{2}b{c}^{3}×4{a}^{4}{b}^{4}{c}^{2}$
=2a6b5c5;
(3)(2x-y)(4x2-y2)(2x+y)
=(2x-y)(2x+y)(4x2-y2)
=(4x2-y2)(4x2-y2)
=16x4-8x2y2+y4;
(4)(54x2y-108xy2-36xy)÷18xy
=3x-6y-2;
(5)(2x+3y)(2x-3y)-(2x+3y)2
=(4x2-9y2)-(4x2+12xy+9y2)
=4x2-9y2-4x2-12xy-9y2
=-12xy-18y2.
点评 本题考查整式的混合运算,解题的关键是明确整式的混合运算的计算方法.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
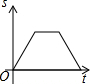
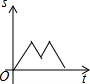
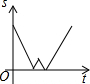
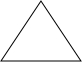 星期天早晨茗茗陪爷爷出门散步,他们所走的路线组成一个等边三角形,如图所示,下列可以正确表示他们离家的距离s与时间t的函数图象的是( )
星期天早晨茗茗陪爷爷出门散步,他们所走的路线组成一个等边三角形,如图所示,下列可以正确表示他们离家的距离s与时间t的函数图象的是( )
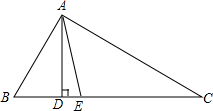 如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.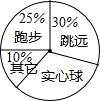 学校为了今年初三年级学生体育中考取得优异的成绩,进行更有针对性的强化训练,体育组为了了解学生最喜欢的考试项目情况,随机抽查了该年级200名学生,调查的结果如图所示.
学校为了今年初三年级学生体育中考取得优异的成绩,进行更有针对性的强化训练,体育组为了了解学生最喜欢的考试项目情况,随机抽查了该年级200名学生,调查的结果如图所示.