题目内容
5.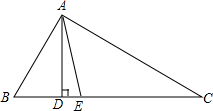 如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
分析 先根据三角形的内角和定理得到∠BAC的度数,再利用角平分线的性质可求出∠BAE=$\frac{1}{2}$∠BAC,而∠BAD=90°-∠B,然后利用∠DAE=∠BAE-∠BAD进行计算即可.
解答 解:在△ABC中,∠B=60°,∠C=30°
∴∠BAC=180°-∠B-∠C=180°-30°-60°=90°
∵AD是的角平分线
∴∠BAE=$\frac{1}{2}$∠BAC=45°,
∵AE是△ABC的高,
∴∠ADB=90°
∴在△ADB中,∠BAD=90°-∠B=90°-60°=30°
∴∠DAE=∠BAE-∠BAD=45°-30°=15°
点评 本题考查了三角形内角和定理.关键是利用三角形内角和定理求解.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
16.下列各组线段中,是成比例线段的是( )
| A. | 1cm,3cm,4cm,6cm | B. | 2cm,3cm,4cm,6cm | ||
| C. | 3cm,5cm,9cm,13cm | D. | 3cm,5cm,9cm,12cm |
13.若x是3的相反数,|y|=2,则x-y的值为( )
| A. | -5 | B. | -1 | C. | -5或-1 | D. | 5或1 |
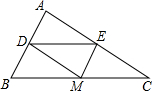 如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是4.8cm.
如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是4.8cm.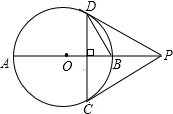 已知AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,CD⊥AB交⊙O于另一点D,连接PD.
已知AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,CD⊥AB交⊙O于另一点D,连接PD.