题目内容
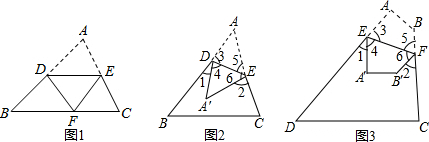
16. 已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.
已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.(1)求证:DG2=GF•GE.
(2)求证:$\frac{C{G}^{2}}{G{A}^{2}}$=$\frac{GF}{GE}$.
分析 (1)运用平行四边形的性质证明:△ADG∽△CFG,△DGC∽△EGA,列出比例式即可解决问题;
(2)由四边形ABCD是平行四边形,得到DC∥AE,证得△CDG∽△AGE,得到$\frac{CG}{AG}=\frac{DG}{GE}$,两边平方得$\frac{C{G}^{2}}{A{G}^{2}}=\frac{D{G}^{2}}{E{G}^{2}}$,通过化简即可得到结论.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,DC∥AE,
∴△ADG∽△CFG,△DGC∽△EGA,
∴DG:GF=AG:GC,GE:DG=AG:GC,
∴DG:GF=GE:DG,
即DG2=GE•GF;
(2)∵四边形ABCD是平行四边形,
∴DC∥AE,
∴△CDG∽△AGE,
∴$\frac{CG}{AG}=\frac{DG}{GE}$,
∴$\frac{C{G}^{2}}{A{G}^{2}}=\frac{D{G}^{2}}{E{G}^{2}}$,
由(1)证得DG2=GE•GF;
∴$\frac{C{G}^{2}}{A{G}^{2}}$=$\frac{GE•GF}{G{E}^{2}}$,
即$\frac{C{G}^{2}}{G{A}^{2}}$=$\frac{GF}{GE}$.
点评 本题考查了平行四边形的性质、相似三角形的判定及其性质,运用平行四边形的性质证明两对相似三角形是解题的关键.

练习册系列答案
相关题目
11.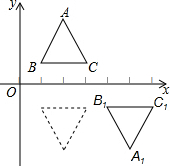 在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
 在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )| A. | (5,-$\sqrt{3}$) | B. | (14,1+$\sqrt{3}$) | C. | (17,-1-$\sqrt{3}$) | D. | (20,1+$\sqrt{3}$) |
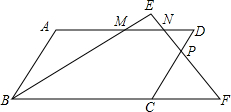 如图,在?ABCD中,M是AD的中点,N是MD的中点,点P在CD上,PN分别与BM、BC的延长线交于点E、F,且DP:PC=1:2.求EN:EF的值.
如图,在?ABCD中,M是AD的中点,N是MD的中点,点P在CD上,PN分别与BM、BC的延长线交于点E、F,且DP:PC=1:2.求EN:EF的值.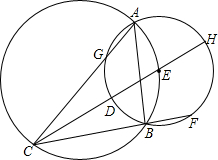 如图,⊙E的圆心在⊙O上,⊙E交⊙O于A、B两点,⊙O的弦CE所在直线交⊙E于点D、H,CB的延长线交⊙E于点F.
如图,⊙E的圆心在⊙O上,⊙E交⊙O于A、B两点,⊙O的弦CE所在直线交⊙E于点D、H,CB的延长线交⊙E于点F.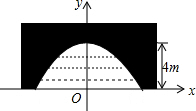 如图是一座古拱桥的截面图,拱桥洞是抛物线形状,其跨度为10m,桥洞与水面的最大距离为4m,将拱桥的横截面放在如图所示的平面直角坐标系中.
如图是一座古拱桥的截面图,拱桥洞是抛物线形状,其跨度为10m,桥洞与水面的最大距离为4m,将拱桥的横截面放在如图所示的平面直角坐标系中.