题目内容
1.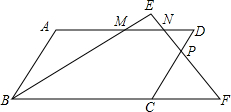 如图,在?ABCD中,M是AD的中点,N是MD的中点,点P在CD上,PN分别与BM、BC的延长线交于点E、F,且DP:PC=1:2.求EN:EF的值.
如图,在?ABCD中,M是AD的中点,N是MD的中点,点P在CD上,PN分别与BM、BC的延长线交于点E、F,且DP:PC=1:2.求EN:EF的值.
分析 先根据平行四边形的性质得AD=BC,AD∥BC,则易得△DNP∽△CFP,利用相似比得$\frac{DN}{CF}$=$\frac{DP}{PC}$=$\frac{1}{2}$,设DN=x,则CF=2x,易得MN=DN=x,AM=MD=2x,AD=BC=4x,所以BF=BC+CF=6x,然后利用MN∥BF判断△EMN∽△EBC,再利用相似比可计算出EN:EF的值.
解答 解:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∵DN∥CF,
∴△DNP∽△CFP,
∴$\frac{DN}{CF}$=$\frac{DP}{PC}$=$\frac{1}{2}$,
设DN=x,则CF=2x,
∵N是MD的中点,M是AD的中点,
∴MN=DN=x,AM=MD=2x,
∴AD=BC=4x,
∴BF=BC+CF=6x,
∵MN∥BF,
∴△EMN∽△EBC,
∴$\frac{EN}{EF}$=$\frac{MN}{BF}$=$\frac{x}{6x}$=$\frac{1}{6}$.
点评 本题考查了相似三角形的判定与性质:三角形相似的判定一直是中考考查的热点之一,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是利用平行线构造相似三角形,然后利用相似三角形的性质进行计算和判断线段之间的关系.也考查了平行四边形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列根式中属最简二次根式的是( )
| A. | $\sqrt{{a}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{10}$ |
13.甲看乙的方向为北偏东60°,那么乙看甲的方向是( )
| A. | 南偏东30° | B. | 南偏西30° | C. | 南偏东60° | D. | 南偏西60° |
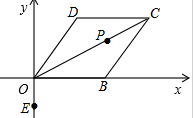 菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),则EP+BP的最小值是$\sqrt{5+2\sqrt{3}}$.
菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),则EP+BP的最小值是$\sqrt{5+2\sqrt{3}}$.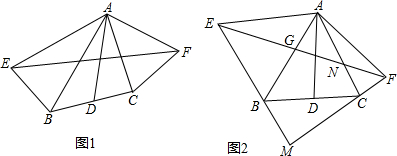
 已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.
已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.