题目内容
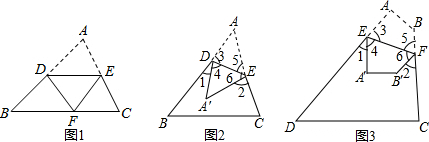
4.(1)如图1,已知D是AB边上的中点,将△ABC沿过点D的直线折叠,使点A落在BC边上的点F处,若∠B=50°,则∠BDF=80°;(2)如图2,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1+∠2=100°,则∠A=50°;
(3)如图3,如果把四边形ABCD沿EF折叠,使点A、B落在四边形EFCD内,试探究∠A+∠B与∠1+∠2之间存在着怎样的数量关系,并证明你的结论.
分析 (1)根据中点的性质和三角形内角和定理计算即可;
(2)根据翻折变换的性质和四边形内角和等于360°计算即可;
(3)与(2)的解答过程相同.
解答 解:(1)∵D是AB边上的中点,
∴AD=DB,又AD=FD,
∴DB=DF,又∠B=50°,
∴∠BDF=80°.
故答案为:80;
(2)∵∠1+∠4+∠3+∠2+∠6+∠5=360°,∠1+∠2=100°,
∴∠4+∠3+∠6+∠5=260°,
∵∠3=∠4,∠5=∠6,
∴∠3+∠5=130°,
∴∠A=50°.
故答案为:50°;
(3)∵∠1+∠4+∠3+∠2+∠6+∠5=360°,
∴∠4+∠3+∠6+∠5=360°-(∠1+∠2),
∵∠3=∠4,∠5=∠6,
∴∠3+∠5=180°-$\frac{1}{2}$(∠1+∠2),
∴∠A+∠B=360°-(∠3+∠5)=180°+$\frac{1}{2}$(∠1+∠2).
点评 本题考查的是翻折变换的性质和三角形内角和定理,找准翻折变换中的对应边和对应角是解题的关键,注意多边形内角和定理的应用.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
13.甲看乙的方向为北偏东60°,那么乙看甲的方向是( )
| A. | 南偏东30° | B. | 南偏西30° | C. | 南偏东60° | D. | 南偏西60° |
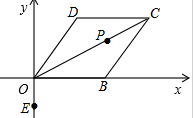 菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),则EP+BP的最小值是$\sqrt{5+2\sqrt{3}}$.
菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),则EP+BP的最小值是$\sqrt{5+2\sqrt{3}}$.
 已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.
已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G. 在长方形ABCD中,放入8个形状和大小都相同的长方形,位置与尺寸如图所示(单位:cm),则阴影部分的面积是112cm2.
在长方形ABCD中,放入8个形状和大小都相同的长方形,位置与尺寸如图所示(单位:cm),则阴影部分的面积是112cm2.