Question

11．在平面直角坐标系中，点（0.5，4）在双曲线y=$\frac{m}{x}$上．
（1）求双曲线的解析式；
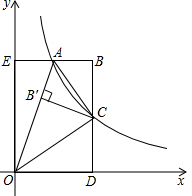
（2）如图，若点A、C分别在矩形ODBE的边EB、BD上，且OC平分∠AOD，双曲线y=$\frac{m}{x}$（x＞0）经过点A、C，将△ABC沿AC折叠得到△AB′C，点B′恰好落在OA上，
①求证：点C是BD的中点．
②求四边形OABC的面积．

Answer 1

分析 （1）把点（0.5，4）代入y=$\frac{m}{x}$，求出m的值，即可得出结果；
（2）①由折叠的性质得出：△△AB′C≌△ABC，得出∠AB′C=∠B，CB′=CB，再由角平分线的性质得出CB′=CD，得出CB=CD即可；
②由C是BD的中点，得出△OCD的面积=$\frac{1}{4}$矩形ODBE的面积，再根据双曲线的解析式求出△OCD的面积=△AOE的面积=1，四边形OABC的面积=矩形ODBE的面积-△OCD的面积-△AOE的面积，即可得出结果．

解答 解：（1）把点（0.5，4）代入y=$\frac{m}{x}$得：m=0.5×4=2，
∴双曲线的解析式为：y=$\frac{2}{x}$；
（2）①证明：根据题意得：△△AB′C≌△ABC，
∴∠AB′C=∠B，CB′=CB，
∵四边形ODBE是矩形，
∴∠ODC=∠B=90°，OD=BE，OE=BD，
∴∠AB′C=∠B=90°，
∵OC平分∠AOD，
∴CB′=CD，
∴CB=CD，
即点C是BD的中点；
②∵四边形ODBE是矩形，C是BD的中点，
∴△OCD的面积=$\frac{1}{4}$矩形ODBE的面积，
∵y=$\frac{2}{x}$，
∴△OCD的面积=△AOE的面积=$\frac{2}{2}$=1，
∴矩形ODBE的面积=4，
∴四边形OABC的面积=矩形ODBE的面积-△OCD的面积-△AOE的面积=4-1-1=2．

点评 本题是反比例函数综合题目，考查了反比例函数解析式的求法、折叠的性质、全等三角形的性质、角平分线的性质以及面积的计算等知识；本题综合性强，有一定难度，熟练掌握矩形的性质和反比例函数，并能进行推理计算是解决问题的关键．