题目内容
1.(1)计算:|-$\sqrt{2}$|+(-$\frac{1}{2}$)-1-2sin45°+($\sqrt{2012}$)0(2)先化简,再求值:($\frac{{a}^{2}-2a+1}{{a}^{2}-1}$+$\frac{1}{a}$)÷$\frac{1}{a+1}$,其中a=$\sqrt{2}$.
分析 (1)原式第一项利用绝对值的代数意义化简,第二项利用负整数指数幂法则计算,第三项利用特殊角的三角函数值计算,最后一项利用零指数幂法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
解答 解:(1)原式=$\sqrt{2}$-2-2×$\frac{\sqrt{2}}{2}$+1=-1;
(2)原式=[$\frac{(a-1)^{2}}{(a+1)(a-1)}$+$\frac{1}{a}$]•(a+1)=($\frac{a-1}{a+1}$+$\frac{1}{a}$)•(a+1)=$\frac{{a}^{2}+1}{a(a+1)}$•(a+1)=$\frac{{a}^{2}+1}{a}$,
当a=$\sqrt{2}$时,原式=$\frac{3}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
9.正六边形的每一个外角都是( )
| A. | 720° | B. | 360° | C. | 120° | D. | 60° |
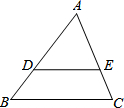 如图,已知D为△ABC边AB上一点,AD=2BD,DE∥BC交AC于E,AE=6,则EC=( )
如图,已知D为△ABC边AB上一点,AD=2BD,DE∥BC交AC于E,AE=6,则EC=( )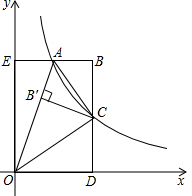 在平面直角坐标系中,点(0.5,4)在双曲线y=$\frac{m}{x}$上.
在平面直角坐标系中,点(0.5,4)在双曲线y=$\frac{m}{x}$上.