题目内容
19. 如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A、B两点,当k=2时;
如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A、B两点,当k=2时;(1)求A、B两点的坐标;
(2)求△AOB的面积.
分析 (1)联立两个函数解析式组成方程组,解方程组求得两函数的交点A、B的坐标;
(2)先根据直线解析式求得直线与y轴的交点C坐标,得到OC的长,再根据△AOB的面积等于△AOC的面积与△BOC的面积的和,进行计算即可.
解答  解:(1)当k=2时,直线解析式为y=x+2,双曲线解析式为$y=\frac{3}{x}$
解:(1)当k=2时,直线解析式为y=x+2,双曲线解析式为$y=\frac{3}{x}$
解方程组$\left\{\begin{array}{l}{y=x+2}\\{y=\frac{3}{x}}\end{array}\right.$,得
$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=-1}\end{array}\right.$
即A(1,3),B(-3,-1)
(2)设直线与y轴交点为C,
在y=x+2中,当x=0时,y=2
∴C(0,2),即OC=2
∴△AOB的面积
=△AOC的面积+△BOC的面积
=$\frac{1}{2}$×CO×|xB|+$\frac{1}{2}$×CO×|xA|
=$\frac{1}{2}$×2×3+$\frac{1}{2}$×2×1
=3+1
=4
点评 本题主要考查了反比例函数与一次函数的交点,解决问题的关键是掌握通过解方程组求两个函数图象交点坐标.当有两个函数的时候,着重使用函数图象的交点坐标以及直线与坐标轴的交点坐标,体现了数形结合思想,综合性较强.在计算△AOB的面积时,也可以将x轴作为分割线,或者将两坐标轴同时作为分割线.

练习册系列答案
相关题目
8.我市某校九年级实行小组合作学习,为了解学生课堂发言情况,随机抽取该年级部分学生,对他们每天在课堂上发言的次数进行调查和统计,统计表如下,并绘制了两幅不完整的统计图,已经知A、B两组发言人数直方图高度比为1:5.
请结E合图中相关的数据回答下列问题:
(1)A组的人数是多少?本次调查的样本容量是多少?
(2)求出C组的人数并补全直方图;
(3)该校七年级共有250人,请估计全年级每天在课堂上发言次数不少于15次的人数.

| 发言次数n | |
| A | 0≤n<5 |
| B | 5≤n<10 |
| C | 10≤n<15 |
| D | 15≤n<20 |
| E | 20≤n<25 |
| F | 25≤n<30 |
(1)A组的人数是多少?本次调查的样本容量是多少?
(2)求出C组的人数并补全直方图;
(3)该校七年级共有250人,请估计全年级每天在课堂上发言次数不少于15次的人数.

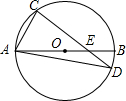 如图,AB为⊙O的直径,弦CD与AB交于点E,连接AD.若∠C=80°,∠CEA=30°,则∠CDA=20°.
如图,AB为⊙O的直径,弦CD与AB交于点E,连接AD.若∠C=80°,∠CEA=30°,则∠CDA=20°. 图中所示的几何体是由一些小立方块搭成的,则这个几何体的主视图是( )
图中所示的几何体是由一些小立方块搭成的,则这个几何体的主视图是( )


