题目内容
15.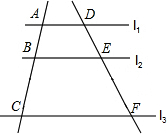 如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=$\frac{8}{5}$.
如图,l1∥l2∥l3,如果AB=2,BC=3,DF=4,那么DE=$\frac{8}{5}$.
分析 由于l1∥l2∥l3,根据平行线分线段成比例得到$\frac{2}{2+3}$=$\frac{DE}{4}$,然后根据比例性质求DE.
解答 解:∵l1∥l2∥l3,
∴$\frac{AB}{AC}$=$\frac{DE}{DF}$,即$\frac{2}{2+3}$=$\frac{DE}{4}$,
∴DE=$\frac{8}{5}$.
故答案为$\frac{8}{5}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
相关题目
5.若将抛物线y=-x2先向右平移2个单位,再向上平移1个单位,则所得抛物线的表达式为( )
| A. | y=-(x-2)2-1 | B. | y=-(x-2)2-1 | C. | y=-(x+2)2-1 | D. | y=-(x-2)2+1 |
6.-6的相反数是( )
| A. | 6 | B. | -6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
3.已知关于x的一元二次方程x2-2x+k=0有两个实数根,则k的值是( )
| A. | k<1 | B. | k≤1 | C. | k>-1 | D. | k≤-1 |
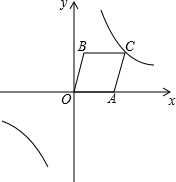 如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y=$\frac{k}{x}$的图象经过点C.
如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y=$\frac{k}{x}$的图象经过点C.