题目内容
20．
在四边形ABCD中，若∠ABC+∠BDC=180°，∠C=∠A，求证：BC=AD．
分析 延长CD至E，使DE=AB，连接BE，证明△ABD≌△EDB，得到∠A=∠E，AD=BE，再证明∠C=∠E，得到BC=BE，所以BC=AD．
解答 解：如图，延长CD至E，使DE=AB，连接BE，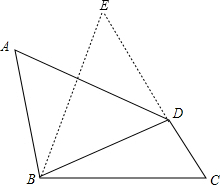
∵∠ABC+∠BDC=180°，
∴∠ABD=∠BDE，
在△ABD和△EDB中，
$\left\{\begin{array}{l}{DE=AB}\\{∠BDE=∠ABD}\\{BD=BD}\end{array}\right.$，
∴△ABD≌△EDB，
∴∠A=∠E，AD=BE，
∵∠C=∠A，
∴∠C=∠E，
∵BC=BE，
∴BC=AD．
点评 本题考查了全等三角形的性质定理与判定定理，解决本题的关键是作出辅助线，构建全等三角形．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
如图，⊙O的直径AB=2，P是上半圆（A、B除外）上任一点，∠APB的平分线交⊙O于C，弦EF过AC、BC的中点M、N，则EF的长是$\sqrt{3}$．
如图，AB为⊙O的直径，AB=2BC=2，DE=DB，则DB=$\frac{\sqrt{2}}{2}$．
如图，OC=OD，PC=PD，PM⊥OC于M，PN⊥OD于N，求证：PM=PN．
如图，抛物线y=-x2+bx+c交x轴于点A（-3，0）和点B，交y轴于点C（0，3）．
9．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表：
下列结论：
（1）abc＜0；
（2）当x＞1时，y的值随x值的增大而减小；
（3）16a+4b+c＜0；
（4）抛物线与坐标轴有两个交点；
（5）x=3是方程ax2+（b-1）x+c=0的一个根；
其中正确的个数为（ ）
| X | -1 | 0 | 1 | 3 |
| y | -$\frac{13}{5}$ | 3 | $\frac{29}{5}$ | 3 |
（1）abc＜0；
（2）当x＞1时，y的值随x值的增大而减小；
（3）16a+4b+c＜0；
（4）抛物线与坐标轴有两个交点；
（5）x=3是方程ax2+（b-1）x+c=0的一个根；
其中正确的个数为（ ）
| A． | 5个 | B． | 4个 | C． | 3个 | D． | 2个 |