题目内容
18.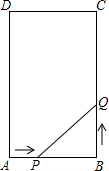 如图所示,在矩形ABCD中,AB=6cm,BC=12cm,点P从A点出发,沿AB边向B点以1cm/s的速度移动,同时点Q从点B出发,沿BC边向点C以2cm/s的速度移动,如果P、Q两点在分别达到B、C两点后就停止移动,回答下列问题:
如图所示,在矩形ABCD中,AB=6cm,BC=12cm,点P从A点出发,沿AB边向B点以1cm/s的速度移动,同时点Q从点B出发,沿BC边向点C以2cm/s的速度移动,如果P、Q两点在分别达到B、C两点后就停止移动,回答下列问题:(1)运动开始后第T秒时,△PBQ的面积等于8cm2.
(2)设运动开始后第T秒时,五边形PQCD的面积为Scm2,写出S与T的函数关系式,并指出自变量T的取值范围;
(3)T为何值时S最小?求出S的最小值.
分析 (1)表示出PB,QB的长,利用△PBQ的面积等于8列式求值即可;
(2)根据t秒时,P、Q两点的运动路程,分别表示PB、BQ的长度,可得△BPQ的面积,用S=S矩形ABCD-S△PBQ求面积即可;
(3)将(1)中所求函数式配方,可得函数的最小值.
解答 解:(1)设x秒后△PBQ的面积等于8cm2.
则AP=x,QB=2x.
∴PB=6-x.
∴$\frac{1}{2}$×(6-x)2x=8,
解得x1=2,x2=4.
答:2秒或4秒后△PBQ的面积等于8cm2.
(2)第t秒钟时,AP=tcm,故PB=(6-t)cm,BQ=2tcm,
故S△PBQ=$\frac{1}{2}$•(6-t)•2t=-t2+6t
∵S矩形ABCD=6×12=72.
∴S=72-S△PBQ=t2-6t+72(0<t<6);
(3)∵S=t2-6t+72=(t-3)2+63,
∴当t=3秒时,S有最小值63cm2.
点评 本题考查了二次函数的最值在解决面积问题中的运用.关键是根据所设字母,表示相关线段的长度,再计算面积,把所得的代数式看作二次函数求最值

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
14.不等式组$\left\{\begin{array}{l}{\frac{1}{2}x+1>0}\\{1-x>0}\end{array}\right.$的解集( )
| A. | x>-2 | B. | x<1 | C. | -2<x<1 | D. | 无解 |
12.等腰三角形ABC中,AB=AC=13,BC=10,则底角B的正切值为( )
| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{5}{12}$ | D. | $\frac{5}{13}$ |
13.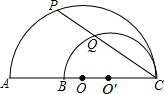 如图,AC、BC是两个半圆的直径,∠ACP=30°,若AB=20cm,则PQ的值为( )
如图,AC、BC是两个半圆的直径,∠ACP=30°,若AB=20cm,则PQ的值为( )
 如图,AC、BC是两个半圆的直径,∠ACP=30°,若AB=20cm,则PQ的值为( )
如图,AC、BC是两个半圆的直径,∠ACP=30°,若AB=20cm,则PQ的值为( )| A. | 10cm | B. | 10$\sqrt{3}$cm | C. | 12cm | D. | 16cm |
 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,则FC=3.
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,则FC=3. 观察图象,当x>4时,y>3?
观察图象,当x>4时,y>3?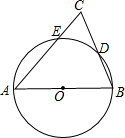 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四种结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是( )
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四种结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是( )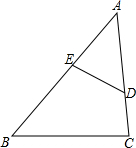 如图,已知D、E分别是△ABC的边AC、AB上的点,若∠A=35°,∠C=85°,∠ADE=60°
如图,已知D、E分别是△ABC的边AC、AB上的点,若∠A=35°,∠C=85°,∠ADE=60°