题目内容
3．在平面直角坐标系中，已知A（1，0 ）、B（1，1 ），现从0、$\frac{1}{2}$、1、2四个数中选两个数分别作为点C的横、纵坐标，则顺次连接A、B、C三点能组成等腰三角形的概率为$\frac{5}{12}$．分析 将所有等可能的结果列举出来，利用概率公式求解即可．
解答 解：从0、$\frac{1}{2}$、1、2四个数中选两个数共有12种组合，
其中能组成等腰三角形的有（0，$\frac{1}{2}$ ）、（0，1）、（2，0）、（2，$\frac{1}{2}$）、（2，1）这5种情况，
则能组成等腰三角形的概率为$\frac{5}{12}$．
点评 考查了列表法与树状图法、等腰三角形的判定等知识，解题的关键是熟练掌握概率公式：概率=所求情况数与总情况数的比值．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
作图题：在图中画出△ABC关于直线l的轴对称图形△A1B1C1．
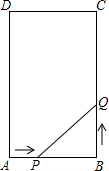如图所示，在矩形ABCD中，AB=6cm，BC=12cm，点P从A点出发，沿AB边向B点以1cm/s的速度移动，同时点Q从点B出发，沿BC边向点C以2cm/s的速度移动，如果P、Q两点在分别达到B、C两点后就停止移动，回答下列问题：
12．小明沿着坡角为30°的坡面向下走了2米，那么他下降（ ）
| A． | 1米 | B． | $\sqrt{3}$米 | C． | 2$\sqrt{3}$米 | D． | $\frac{2\sqrt{3}}{3}$米 |