题目内容
7.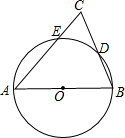 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四种结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是( )
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四种结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是( )| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
分析 连接AD,根据圆周角定理可知∠ADB=90°,再由CD=CB可知AD是BC的垂直平分线,可知②正确;连接DE,BE,由圆内接四边形的性质可知∠CDE=∠CAB,故可得出△CDE∽△CAB,由此可判断出④正确.
解答 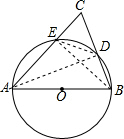 解:连接AD,
解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°.
∵CD=BD,
∴AD是BC的垂直平分线,
∴AC=AB,故②正确;
∵AC=AB,
∴∠ABC=∠C=70°,
∴∠BAC=40°,故①错误;
连接BE,DE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵∠BAC=40°,
∴∠ABE=50°,
∴∠BAC≠∠ABE,
∴AE≠BE,故③错误;
∵四边形ABDE是圆内接四边形,
∴∠CDE=∠CAB,
∴△CDE∽△CAB,
∴$\frac{CD}{AC}$=$\frac{CE}{BC}$,即$\frac{BD}{AB}=\frac{CE}{2BD}$,
∴CE•AB=2BD2,故④正确.
故选C.
点评 本题考查了相似三角形的判定和性质,圆周角定理,根据题意作出辅助线,构造出圆周角是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
12.小明沿着坡角为30°的坡面向下走了2米,那么他下降( )
| A. | 1米 | B. | $\sqrt{3}$米 | C. | 2$\sqrt{3}$米 | D. | $\frac{2\sqrt{3}}{3}$米 |
19.在下列四组点中,可以在同一个正比例函数图象上的一组点是( )
| A. | (-2,-3),(4,-6) | B. | (-2,3),(4,6) | C. | (2,-3),(-4,6) | D. | (2,3),(-4,6) |
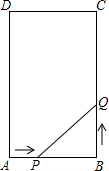 如图所示,在矩形ABCD中,AB=6cm,BC=12cm,点P从A点出发,沿AB边向B点以1cm/s的速度移动,同时点Q从点B出发,沿BC边向点C以2cm/s的速度移动,如果P、Q两点在分别达到B、C两点后就停止移动,回答下列问题:
如图所示,在矩形ABCD中,AB=6cm,BC=12cm,点P从A点出发,沿AB边向B点以1cm/s的速度移动,同时点Q从点B出发,沿BC边向点C以2cm/s的速度移动,如果P、Q两点在分别达到B、C两点后就停止移动,回答下列问题: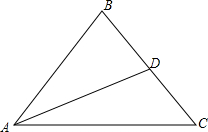 (1)已知点A(m+1,2n-3)关于原点对称的点A1(2m+1,-n-1),求m、n的值.
(1)已知点A(m+1,2n-3)关于原点对称的点A1(2m+1,-n-1),求m、n的值. 如图,在△ABC与△ABD中,AD与BC相交于0点,∠1=∠2,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AC=BD.并给出证明.
如图,在△ABC与△ABD中,AD与BC相交于0点,∠1=∠2,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AC=BD.并给出证明.