题目内容
13．
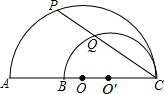如图，AC、BC是两个半圆的直径，∠ACP=30°，若AB=20cm，则PQ的值为（ ）| A． | 10cm | B． | 10$\sqrt{3}$cm | C． | 12cm | D． | 16cm |
分析 连接BQ，AP，如图，由于AC，BC为直径，根据圆周角定理得∠APC=90°，∠BQC=90°，再根据含30度的直角三角形三边的关系得到PC=$\frac{\sqrt{3}}{2}$AC，CQ=$\frac{\sqrt{3}}{2}$BC，PQ=PC-CQ=$\frac{\sqrt{3}}{2}$（AC-BC）=$\frac{\sqrt{3}}{2}$AB=10$\sqrt{3}$．
解答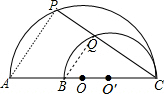 
解：连接BQ，AP，如图，
∵AC，BC为直径，
∴∠APC=90°，∠BQC=90°，
∵∠ACP=30°，
∴PC=$\frac{\sqrt{3}}{2}$AC，CQ=$\frac{\sqrt{3}}{2}$BC，
∴PQ=PC-CQ=$\frac{\sqrt{3}}{2}$（AC-BC）=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$×20=10$\sqrt{3}$（cm）．
故选B．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，一条弧所对的圆周角的度数等于它所对的圆心角度数的一半．也考查了平行线的性质以及直径所对的圆周角为直角．
练习册系列答案
相关题目
9．一个直角三角形的直角边长分别为3和5，第三边的长是方程x2-6x+8=0的根，则这个三角形的周长为（ ）
| A． | 10 | B． | 12 | C． | 10或12 | D． | 以上都不对 |
8．
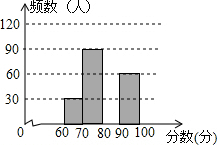为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况，随机抽取了部分参赛同学的成绩，整理并制作如图所示的图表（部分未完成）．请你根据表中提供的信息，解答下列问题：
（1）此次调查的样本容量为300；m=120；n=0.3；
（2）补全频数分布直方图；
（3）如果比赛成绩80分以上为优秀，那么你估计师大附中多元校区八年级学生笔试成绩的优秀人数大约是1800名．
为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况，随机抽取了部分参赛同学的成绩，整理并制作如图所示的图表（部分未完成）．请你根据表中提供的信息，解答下列问题：| 分数段 | 频数 | 频率 |
| 60≤x＜70 | 30 | 0.1 |
| 70≤x＜80 | 90 | n |
| 80≤x＜90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
（2）补全频数分布直方图；
（3）如果比赛成绩80分以上为优秀，那么你估计师大附中多元校区八年级学生笔试成绩的优秀人数大约是1800名．
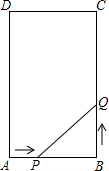如图所示，在矩形ABCD中，AB=6cm，BC=12cm，点P从A点出发，沿AB边向B点以1cm/s的速度移动，同时点Q从点B出发，沿BC边向点C以2cm/s的速度移动，如果P、Q两点在分别达到B、C两点后就停止移动，回答下列问题：
5．下列运算中，正确的是（ ）
| A． | $\sqrt{9}=±3$ | B． | （a2）3=a6 | C． | 3a•2a=6a | D． | 3-2=-6 |
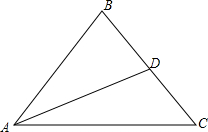（1）已知点A（m+1，2n-3）关于原点对称的点A1（2m+1，-n-1），求m、n的值．