题目内容
8．
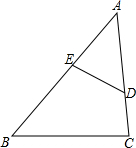如图，已知D、E分别是△ABC的边AC、AB上的点，若∠A=35°，∠C=85°，∠ADE=60°（1）请说明：△ADE∽△ABC；
（2）若AD=8，AE=6，BE=10，求AC的长．
分析 （1）根据三角形内角和定理求出∠B，推出∠B=∠ADE，根据相似三角形的判定得出即可；
（2）根据相似三角形的性质得出比例式，代入求出即可．
解答 解：（1）∵∠A=35°，∠C=85°，
∴∠B=180°-∠A-∠C=60°，
∵∠ADE=60°，
∴∠B=∠ADE，
∵∠A=∠A，
∴△ADE∽△ABC；
（2）∵△ADE∽△ABC，
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$，
∵AD=8，AE=6，BE=10，
∴$\frac{6}{AC}$=$\frac{8}{6+10}$，
∴AC=12．
点评 本题考查了三角形内角和定理，相似三角形的性质和判定的应用，能推出△ADE∽△ABC是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
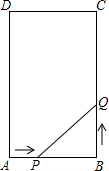如图所示，在矩形ABCD中，AB=6cm，BC=12cm，点P从A点出发，沿AB边向B点以1cm/s的速度移动，同时点Q从点B出发，沿BC边向点C以2cm/s的速度移动，如果P、Q两点在分别达到B、C两点后就停止移动，回答下列问题：
19．在下列四组点中，可以在同一个正比例函数图象上的一组点是（ ）
| A． | （-2，-3），（4，-6） | B． | （-2，3），（4，6） | C． | （2，-3），（-4，6） | D． | （2，3），（-4，6） |
如图，在△ABC与△ABD中，AD与BC相交于0点，∠1=∠2，请你添加一个条件（不再添加其他线段，不再标注或使用其他字母），使AC=BD．并给出证明．