Question

6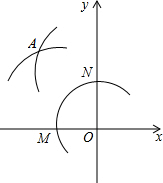．在平面直角坐标系中，在x轴的负半轴与y轴的正半轴上分别截取OM，ON，使OM=ON；再分别以点M，N为圆心、大于$\frac{1}{2}$MN长为半径作弧，两弧在第二象限交于点A，若点A的坐标为（$\frac{m+1}{2}$，$\frac{m+9}{3}$-1），求点A的坐标．

Answer 1

分析 利用基本作图可判断OA为角平分线，则利用角平分线的性质得到-$\frac{m+1}{2}$=$\frac{m+9}{3}$-1，然后解方程求出m即可得到A点坐标．

解答 解：作图可得点A在第二象限的角平分线上，
则-$\frac{m+1}{2}$=$\frac{m+9}{3}$-1，解得m=-3，
所以A点坐标为（-1，1）．

点评 本题考查了基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．