题目内容
20.分解因式:(1)ax2-7ax+6a;
(2)9a2(x-y)+4b2(y-x);
(3)2(x-3)(x-1)+2;
(4)x2y2-x2-4y2+4xy.
分析 (1)先提公因式,再分解即可;
(2)先变形,再提公因式,再根据平方差公式分解即可;
(3)整理后再提公因式,再根据完全平方公式分解即可;
(4)先分组,再根据平方差公式分解即可.
解答 解:(1)ax2-7ax+6a
=a(x2-7x+6)
=a(x-1)(x-6);
(2)9a2(x-y)+4b2(y-x)
=9a2(x-y)-4b2(x-y)
=(x-y)(9a2-4b2)
=(x-y)(3a+2b)(3a-2b);
(3)2(x-3)(x-1)+2
=2x2-8x+8
=2(x2-4x+4)
=2(x-2)2;
(4)x2y2-x2-4y2+4xy
=x2y2-(x2-4xy+4y2)
=(xy)2-(x-2y)2
=(xy+x-2y)(xy-x+2y).
点评 本题考查了分解因式,能灵活运用因式分解的各种方法分解因式是解此题的关键.

练习册系列答案
相关题目
10.已知函数y=k(x+1)(x-$\frac{3}{k}$),下列说法正确的是( )
| A. | 方程k(x+1)(x-$\frac{3}{k}$)=-3必有实数根 | |
| B. | 若移动函数图象使其经过原点,则只能将图象向右移动1个单位 | |
| C. | 若k>0,则当x>0时,必有y随着x的增大而增大 | |
| D. | 若k<0,则当x<-1时,必有y随着x的增大而增大 |

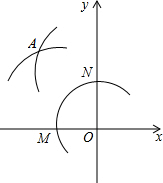 在平面直角坐标系中,在x轴的负半轴与y轴的正半轴上分别截取OM,ON,使OM=ON;再分别以点M,N为圆心、大于$\frac{1}{2}$MN长为半径作弧,两弧在第二象限交于点A,若点A的坐标为($\frac{m+1}{2}$,$\frac{m+9}{3}$-1),求点A的坐标.
在平面直角坐标系中,在x轴的负半轴与y轴的正半轴上分别截取OM,ON,使OM=ON;再分别以点M,N为圆心、大于$\frac{1}{2}$MN长为半径作弧,两弧在第二象限交于点A,若点A的坐标为($\frac{m+1}{2}$,$\frac{m+9}{3}$-1),求点A的坐标. 如图,在四边形ABCD中,∠A=90°,AB=5,AD=3,点M在边AB上,则DM的最大值为$\sqrt{34}$.
如图,在四边形ABCD中,∠A=90°,AB=5,AD=3,点M在边AB上,则DM的最大值为$\sqrt{34}$.