题目内容
用一根长40m的篱笆围成一个矩形场地，长和宽分别为多少时，面积最大？
考点：二次函数的最值
专题：
分析：设长方形的长为xm，表示出宽，然后根据长方形的面积公式列式整理，再根据二次函数的最值问题解答．
解答：解：设长方形的长为xm，则宽为（20-x）m，
长方形的面积=x（20-x）=-x2+20x=-（x-10）2+100，
所以，当x=10m时，面积最大，最大面积为100m2，
此时宽为20-10=10m，
答：长和宽分别为10m、10m时，面积最大．
长方形的面积=x（20-x）=-x2+20x=-（x-10）2+100，
所以，当x=10m时，面积最大，最大面积为100m2，
此时宽为20-10=10m，
答：长和宽分别为10m、10m时，面积最大．
点评：本题考查了二次函数的最值，用长表示出宽然后列出面积的表达式是解题的关键，整理成顶点式形式求解更简便．
练习册系列答案
口算题天天练系列答案
相关题目
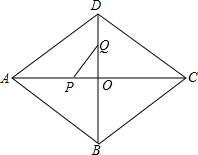如图，在菱形ABCD中，AC、BD交于点O，AD=15，AO=12．动点P以每秒2个单位的速度从点A出发，沿AC向点C匀速运动．同时，动点Q以每秒1个单位的速度从点D出发，沿DB向点B匀速运动．当其中有一点到达终点时，另一点也停止运动．设运动的时间为t秒．