题目内容
1.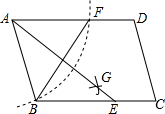 如图,用直尺和圆规作∠BAD的平分线AG,过点B作BC∥AD,交AG于点E,BF=6,AB=5,则AE的长为( )
如图,用直尺和圆规作∠BAD的平分线AG,过点B作BC∥AD,交AG于点E,BF=6,AB=5,则AE的长为( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
分析 由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=$\frac{1}{2}$BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
解答 解:连结EF,AE与BF交于点O,如图,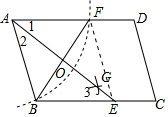
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=$\frac{1}{2}$BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AE=2AO=8.
故选:B.
点评 本题考查了平行四边形的性质:平行四边形的对边相等、平行四边形的对角相等、平行四边形的对角线互相平分.也考查了等腰三角形的判定与性质和基本作图.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下面每组数分别是三根小木棒的长度(单位:cm),用它们能摆成三角形的是( )
| A. | 3,4,8 | B. | 12,13,5 | C. | 7,8,15 | D. | 1,6,3 |
9.要使分式$\frac{2}{x+1}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x<1 | D. | x≠-1 |
16.在数轴上把-3的对应点移动5个单位后,所得的对应点表示的数是( )
| A. | 2或-8 | B. | -8 | C. | 2 | D. | 不能确定 |
11.下面四个结论,正确的是( )
| A. | 单项式-34a2b5的次数是11次 | |
| B. | 已知a是有理数,且|a|=-a,则有理数a在数轴上的对应点在原点的左边 | |
| C. | 无理数的绝对值一定是非负数 | |
| D. | 延长线段BA到C,使AC=2BC |
 如图,已知点C为AB上一点,AC=12cm,BC=$\frac{2}{3}$AC,D,E分别为AC,AB的中点,求DE的长.
如图,已知点C为AB上一点,AC=12cm,BC=$\frac{2}{3}$AC,D,E分别为AC,AB的中点,求DE的长.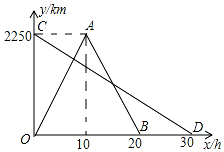 一辆快车和一辆慢车分别从甲、乙两地同时出发匀速相向而行,快车到达乙地后,原路原速返回甲地.图1表示两车行驶过程中离甲地的路程y(km)与行驶时间x(h)的函数图象.
一辆快车和一辆慢车分别从甲、乙两地同时出发匀速相向而行,快车到达乙地后,原路原速返回甲地.图1表示两车行驶过程中离甲地的路程y(km)与行驶时间x(h)的函数图象. 在平面直角坐标系xOy中,有一点C,过点C分别作CA⊥x轴,CB⊥y轴,点A、B是垂足.
在平面直角坐标系xOy中,有一点C,过点C分别作CA⊥x轴,CB⊥y轴,点A、B是垂足.