题目内容
3.要得到y=-5(x-2)2+3的图象,将抛物线y=-5x2作如下平移( )| A. | 向右平移2个单位,再向上平移3个单位 | |
| B. | 向右平移2个单位,再向下平移3个单位 | |
| C. | 向左平移2个单位,再向上平移3个单位 | |
| D. | 向左平移2个单位,再向下平移3个单位 |
分析 先确定抛物线y=-5x2的顶点坐标为(0,0),抛物线y=-5(x-2)2+3的顶点坐标为(2,3),根据点平移的规律得到点(0,0)先向右平移2个单位,再向上平移3个单位得到点(2,3),于是可判断抛物线平移的方向与单位.
解答 解:抛物线y=-5x2的顶点坐标为(0,0),而抛物线y=-5(x-2)2+3的顶点坐标为(2,3),
因为点(0,0)先向右平移2个单位,再向上平移3个单位得到点(2,3),
所以把抛物线抛物线y=-5x2先向右平移2个单位,再向上平移3个单位得到抛物线y=-5(x-2)2+3.
故选A.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列计算正确的是( )
| A. | (x2)3=x5 | B. | x6+x6=x12 | C. | x2•x3=x5 | D. | (2x)2=2x2 |
11.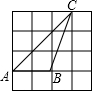 如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
 如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
如图,小正方形的边长均为1,有格点△ABC,则sinC=( )| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
8.以下列各组数据为三角形三边,能构成直角三角形的是( )
| A. | 4,8,7 | B. | 5,12,14 | C. | 2,2,4 | D. | 7,24,25 |
15.两个三次三项式的和是( )
| A. | 六次多项式 | B. | 不超过三次的六项式 | ||
| C. | 不超过三次的多项式 | D. | 不超过六项的三次多项式 |
13.相同时刻太阳光下,若高为1.5m的测杆的影长为3m,则影长为30m的旗杆的高是( )
| A. | 15m | B. | 16m | C. | 18m | D. | 20m |
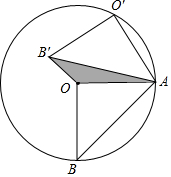 如图,在Rt△AOB中,∠AOB=Rt∠,OA=OB=2,将△AOB绕点A按顺时针旋转至△AO′B′,使点O′落在以O为圆心,OA长为半径的圆上,则△AOB′的面积是$\sqrt{3}$-1.
如图,在Rt△AOB中,∠AOB=Rt∠,OA=OB=2,将△AOB绕点A按顺时针旋转至△AO′B′,使点O′落在以O为圆心,OA长为半径的圆上,则△AOB′的面积是$\sqrt{3}$-1.