题目内容
12.计算:$\sqrt{\frac{8}{9}}$+$\sqrt{8}$的结果为$\frac{8}{3}$$\sqrt{2}$.分析 先进行二次根式的化简,再进行二次根式的加减法运算求解即可.
解答 解:原式=$\frac{\sqrt{8}}{3}$+$\sqrt{8}$
=$\frac{2\sqrt{2}}{3}$+2$\sqrt{2}$
=$\frac{8}{3}$$\sqrt{2}$.
故答案为:$\frac{8}{3}$$\sqrt{2}$.
点评 本题考查了二次根式的加减法,解答本题的关键在于熟练掌握二次根式的化简及二次根式加减法运算法则.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
2.已知数轴上A、B表示的数互为相反数,并且两点间的距离是8,点A在点B的左边,则点A、B表示的数分别是( )
| A. | -4,4 | B. | 4,-4 | C. | 8,-8 | D. | -8,8 |
3.要得到y=-5(x-2)2+3的图象,将抛物线y=-5x2作如下平移( )
| A. | 向右平移2个单位,再向上平移3个单位 | |
| B. | 向右平移2个单位,再向下平移3个单位 | |
| C. | 向左平移2个单位,再向上平移3个单位 | |
| D. | 向左平移2个单位,再向下平移3个单位 |
20.方程x2-3x+4=0和2x2-4x-3=0所有实数根的和是( )
| A. | 3 | B. | 5 | C. | 1 | D. | 2 |
4.下列函数是反比例函数的是( )
| A. | y=-2x | B. | y=-$\frac{2}{x}$ | C. | y=-$\frac{x}{2}$ | D. | y=x2-1 |
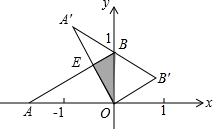 如图,点A的坐标为(-$\sqrt{3}$,0),点B的坐标为(0,1),将△AOB绕原点O顺时针旋转60°到△A'OB',A'B'恰好过点B,则B'的坐标为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),重叠部分△BOE的面积为$\frac{\sqrt{3}}{8}$.
如图,点A的坐标为(-$\sqrt{3}$,0),点B的坐标为(0,1),将△AOB绕原点O顺时针旋转60°到△A'OB',A'B'恰好过点B,则B'的坐标为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),重叠部分△BOE的面积为$\frac{\sqrt{3}}{8}$.