题目内容
11．
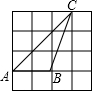如图，小正方形的边长均为1，有格点△ABC，则sinC=（ ）| A． | $\frac{2}{3}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
分析 连接BD，根据正方形的性质得到，∠CDB=90°，BD=$\sqrt{2}$，BC=$\sqrt{10}$，根据正弦的定义计算即可．
解答 解：
如图，连接BD，
由正方形的性质可知，∠CDB=90°，BD=$\sqrt{2}$，BC=$\sqrt{10}$，
则sinC=$\frac{BD}{BC}$=$\frac{\sqrt{5}}{5}$，
故选：B．
点评 本题考查的是锐角三角函数的定义、正方形的性质，掌握锐角A的对边a与斜边c的比叫做∠A的正弦是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．股民小王上周五收盘前买进某支股票2000股，每股28元．表为本周内该股票的涨跌情况：
（1）将表中空缺单元格填写完整；
（2）本周内，收盘时的最高价与最低价相差多少？
（3）已知买进股票时需要付成交额0.15%的交易费，卖出股票时需要付成交额0.15%的交易费和0.1%的印花税．如果小王在本周收盘时将全部股票一次性卖出，那么小王的收益情况如何？
| 时间 | 一 | 二 | 三 | 四 | 五 |
| 收盘价（元/股） | 27.2 | 29 | |||
| 比前一天涨跌（元/股） | -0.2 | +1.2 | +1 |
（2）本周内，收盘时的最高价与最低价相差多少？
（3）已知买进股票时需要付成交额0.15%的交易费，卖出股票时需要付成交额0.15%的交易费和0.1%的印花税．如果小王在本周收盘时将全部股票一次性卖出，那么小王的收益情况如何？
2．已知数轴上A、B表示的数互为相反数，并且两点间的距离是8，点A在点B的左边，则点A、B表示的数分别是（ ）
| A． | -4，4 | B． | 4，-4 | C． | 8，-8 | D． | -8，8 |
6．已知二次函数y=ax2，下列说法正确的是（ ）
| A． | 当a＞0，x≠0时，y总取负值 | |
| B． | 当a＜0，x＜0时，y随x的增大而减小 | |
| C． | 当a＜0时，函数图象有最低点，y有最小值 | |
| D． | 当a＞0，x＞0时，图象在第一象限 |
3．要得到y=-5（x-2）2+3的图象，将抛物线y=-5x2作如下平移（ ）
| A． | 向右平移2个单位，再向上平移3个单位 | |
| B． | 向右平移2个单位，再向下平移3个单位 | |
| C． | 向左平移2个单位，再向上平移3个单位 | |
| D． | 向左平移2个单位，再向下平移3个单位 |
20．方程x2-3x+4=0和2x2-4x-3=0所有实数根的和是（ ）
| A． | 3 | B． | 5 | C． | 1 | D． | 2 |
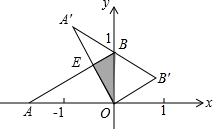如图，点A的坐标为（-$\sqrt{3}$，0），点B的坐标为（0，1），将△AOB绕原点O顺时针旋转60°到△A'OB'，A'B'恰好过点B，则B'的坐标为（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$），重叠部分△BOE的面积为$\frac{\sqrt{3}}{8}$．