题目内容
已知⊙O的面积为3π，则其内接正方形的边长为（ ）
| A、3 | ||
B、
| ||
C、
| ||
D、
|
考点：正多边形和圆
专题：
分析：如图，作辅助线，根据圆的面积公式求出半径；根据勾股定理求出边长问题即可解决．
解答：
解：如图，四边形ABCD为⊙O的内接正方形，连接AC、BD；
设⊙O的半径为λ，则πλ2=3π，
∴λ=
；
又∵∠ABC=90°，
∴AC为⊙O的直径，AC=2λ=2
；
设正方形ABCD的边长为μ，由勾股定理得：
μ2+μ2=(2
)2，
∴μ=
，
故选B．
解：如图，四边形ABCD为⊙O的内接正方形，连接AC、BD；设⊙O的半径为λ，则πλ2=3π，
∴λ=
| 3 |
又∵∠ABC=90°，
∴AC为⊙O的直径，AC=2λ=2
| 3 |
设正方形ABCD的边长为μ，由勾股定理得：
μ2+μ2=(2
| 3 |
∴μ=
| 6 |
故选B．
点评：该题主要考查了圆内接正多边形的性质及其应用问题；解题的关键是灵活运用有关定理，大胆推测、科学论证、准确解答．
练习册系列答案
相关题目
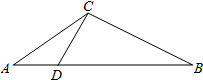D为△ABC中AB边上一点，∠ACD=∠ABC．求证：AC2=AD•AB．
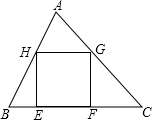如下图，在△ABC中，正方形EFGH的两个顶点E、F在BC上，另两个顶点G、H分别在AC、AB上，BC=15，BC边上的高是10，则正方形的面积为（ ）