题目内容
已知二次函数y=x2+2mx+3,当x<2时,y随x的增大而减小,实数m的取值范围是 .
考点:二次函数的性质
专题:计算题
分析:先把解析式配成顶点式得到y=(x+m)2+3-m2,则抛物线的对称轴为直线x=-m,根据二次函数的性质得当x<-m时,y随x的增大而减小,所以-m≥2,然后解不等式即可.
解答:解:y=x2+2mx+3
=(x+m)2+3-m2,
抛物线的对称轴为直线x=-m,
因为抛物线开口向上,
所以当x<-m时,y随x的增大而减小,
又因为x<2时,随x的增大而减小,
所以-m≥2,解得m≤-2.
故答案为m≤-2.
=(x+m)2+3-m2,
抛物线的对称轴为直线x=-m,
因为抛物线开口向上,
所以当x<-m时,y随x的增大而减小,
又因为x<2时,随x的增大而减小,
所以-m≥2,解得m≤-2.
故答案为m≤-2.
点评:本题考查而次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知⊙O的面积为3π,则其内接正方形的边长为( )
| A、3 | ||
B、
| ||
C、
| ||
D、
|
若m>0,n<0,则一定有( )
| A、m-|n|>0 |
| B、m+n>0 |
| C、m2+n3>0 |
| D、n2+m3>0 |
已知C是线段AB的黄金分割点,AC<BC,若AB=2,则BC=( )
A、
| ||||
B、
| ||||
C、3-
| ||||
D、
|
 如图,二次函数y=ax2+bx+4的图象交于A、B两点,与y轴交于点C,则代数式4a+2b+4的值是( )
如图,二次函数y=ax2+bx+4的图象交于A、B两点,与y轴交于点C,则代数式4a+2b+4的值是( )
 已知:如图,A、C、F、D在同一直线上,AF=CD,AB=DE,BC=EF,求证:∠B=∠E.
已知:如图,A、C、F、D在同一直线上,AF=CD,AB=DE,BC=EF,求证:∠B=∠E.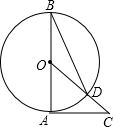 已知,如图所示,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.求∠ABD的度数.
已知,如图所示,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.求∠ABD的度数.