题目内容
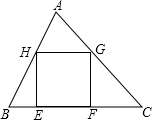如下图，在△ABC中，正方形EFGH的两个顶点E、F在BC上，另两个顶点G、H分别在AC、AB上，BC=15，BC边上的高是10，则正方形的面积为（ ）| A、6 | B、36 | C、12 | D、49 |
考点：相似三角形的判定与性质
专题：
分析：过A作AI⊥BC交BC于I，交HG于K，设正方形EFGH的边长为x，则HG=HE=IK=x，根据题意可得
=
，且AK=AI-x，代入可求得x，进一步可求得面积．
| AK |
| AI |
| HG |
| BC |
解答：解：
过A作AI⊥BC交BC于I，交HG于K，设正方形EFGH的边长为x，则HG=HE=IK=x，
∵HG∥BC，
∴
=
，且AK=AI-x，
又∵AI=10，BC=15，
∴
=
，
解得x=6，
∴S正方形EFGH=x2=36．
故选B．
过A作AI⊥BC交BC于I，交HG于K，设正方形EFGH的边长为x，则HG=HE=IK=x，
∵HG∥BC，
∴
| AK |
| AI |
| HG |
| BC |
又∵AI=10，BC=15，
∴
| 10-x |
| 10 |
| x |
| 15 |
解得x=6，
∴S正方形EFGH=x2=36．
故选B．
点评：本题主要考查平行线分线段成比例的性质，掌握平行线分线段中的线段对应成比例是解题的关键，注意方程思想的应用．
练习册系列答案
相关题目
如图，已知△ABC中CE⊥AB于E，BF⊥AC于F，已知⊙O的面积为3π，则其内接正方形的边长为（ ）
| A、3 | ||
B、
| ||
C、
| ||
D、
|
如图，△ABC是等边三角形，P是三角形外的一点，且∠ABP+∠ACP=180°．求证：PB+PC=PA．