题目内容
若抛物线y=x2+bx+c与x轴只有一个交点，且过点A（1，n），B（7，n），则n= ．
考点：抛物线与x轴的交点,二次函数图象上点的坐标特征
专题：
分析：根据点A、B的坐标易求该抛物线的对称轴是x=4．故设抛物线解析式为y=（x-4）2，直接将A（1，n）代入，通过解方程来求n的值．
解答：解：∵抛物线y=x2+bx+c过点A（1，n）、B（7，n），
∴对称轴是x=4．
又∵抛物线y=x2+bx+c与x轴只有一个交点，
∴设抛物线解析式为y=（x-4）2，
把A（1，n）代入，得
n=（1-4）2=9，即n=9．
故答案是：9．
∴对称轴是x=4．
又∵抛物线y=x2+bx+c与x轴只有一个交点，
∴设抛物线解析式为y=（x-4）2，
把A（1，n）代入，得
n=（1-4）2=9，即n=9．
故答案是：9．
点评：本题考查了抛物线与x轴的交点．解答该题的技巧性在于找到抛物线的顶点坐标，根据顶点坐标设抛物线的解析式．
练习册系列答案
名校课堂系列答案
相关题目
已知⊙O的面积为3π，则其内接正方形的边长为（ ）
| A、3 | ||
B、
| ||
C、
| ||
D、
|
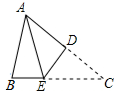如图，将三角形纸片ABC折叠，使点C与点A重合，折痕为DE．若∠B=82°，∠BAE=26°，则∠EAD的度数为（ ）| A、28° | B、30° |
| C、36° | D、45° |
已知：如图，A、C、F、D在同一直线上，AF=CD，AB=DE，BC=EF，求证：∠B=∠E．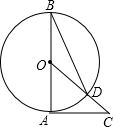
已知，如图所示，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D，连接BD，∠C=40°．求∠ABD的度数．