题目内容
8.已知,关于x,y的方程组$\left\{\begin{array}{l}{x-y=a+3}\\{2x+y=5a}\end{array}\right.$的解满足x<y<0.(1)求a的取值范围;
(2)化简|a|-|a+3|.
分析 (1)根据方程组$\left\{\begin{array}{l}{x-y=a+3}\\{2x+y=5a}\end{array}\right.$,可以用关于a的代数式表示出x、y,然后根据x<y<0,可以求得a的取值范围;
(2)根据(1)中a的取值范围可以对|a|-|a+3|进行化简.
解答 解:(1)$\left\{\begin{array}{l}{x-y=a+3}\\{2x+y=5a}\end{array}\right.$
解得,$\left\{\begin{array}{l}{x=2a+1}\\{y=a-2}\end{array}\right.$,
∵x<y<0,
∴$\left\{\begin{array}{l}{2a+1<a-2}\\{a-2<0}\end{array}\right.$
解得,a<-3,
即a的取值范围是a<-3;
(2)∵a<-3,
∴a+3<0,
∴|a|-|a+3|
=-a+a+3
=3.
点评 本题考查二元一次方程组组的解,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
18.以下列各组数为边长,不能构成直角三角形的是( )
| A. | 1、2、$\sqrt{5}$ | B. | 1、$\sqrt{3}$、2 | C. | 3、4、5 | D. | 6、8、12 |
16.计算:(ab3)2=( )
| A. | a2b2 | B. | a2b3 | C. | ab6 | D. | a2b6 |
20.已知一次函数y=ax+b在平面直角坐标系中的图案经过第一、二、三象限,则下列对a、b的符号判断正确的是( )
| A. | a<0,b<0 | B. | a>0,b>0 | C. | a>0,b<0 | D. | a<0,b>0 |
17.若2(a+3)的值与4互为相反数,则a的值为( )
| A. | -1 | B. | -$\frac{7}{2}$ | C. | -5 | D. | $\frac{1}{2}$ |
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为28°.
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为28°. 如图,已知BE=CD,要使△ABE≌△ACD,要添加一个条件是∠B=∠C.(只填一种情况).
如图,已知BE=CD,要使△ABE≌△ACD,要添加一个条件是∠B=∠C.(只填一种情况).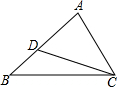 如图,在△ABC中,AB=10,AC=8,点D在边AB上,若∠ACD=∠B,则AD的长为6.4.
如图,在△ABC中,AB=10,AC=8,点D在边AB上,若∠ACD=∠B,则AD的长为6.4.