题目内容
5. 如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.
如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.(1)用尺规作图方法,作∠ADC的平分线DN(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状并给出证明.
分析 (1)利用基本作图(作已知角的平分线)作DN平分∠ADC;
(2)根据等腰三角形的性质得∠BAD=∠CAD,再利用AM是△ABC外角∠CAE的平分线可得∠FAD=90°,则可判断AF∥BC,利用平行线的性质得∠CDF=∠AFD,加上∠AFD=∠ADF,所以∠CDF=∠ADF,然后根据等腰三角形的判定方法可得到△ADF是等腰直角三角形.
解答 解:(1)如图,DN为所作;
(2)△ADF是等腰直角三角形.
理由如下:∵AB=AC,AD是高,
∴∠BAD=∠CAD,
又∵AM是△ABC外角∠CAE的平分线,
∴∠FAD=$\frac{1}{2}$×180°=90°,
∴AF∥BC,
∴∠CDF=∠AFD,
又∵∠AFD=∠ADF,
∴∠CDF=∠ADF,
∴AD=AF,
∴△ADF是等腰直角三角形.
点评 本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了等腰三角形的判断与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.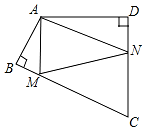 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )| A. | 135° | B. | 130° | C. | 125° | D. | 120° |
10.在函数$y=\frac{x-1}{{\sqrt{4-x}}}$中,自变量x的取值范围是( )
| A. | x≠4 | B. | x≤4 | C. | x<4 | D. | 1<x<4 |
 一个圆柱体钢块,正中央被挖去了一个长槽,其俯视图如图所示,则此圆柱体钢块的左视图是( )
一个圆柱体钢块,正中央被挖去了一个长槽,其俯视图如图所示,则此圆柱体钢块的左视图是( )



 如图,梯形ABCD中,AD∥BC,∠B=45°,∠D=120°,AB=6cm,则DC的长为2$\sqrt{6}$cm.
如图,梯形ABCD中,AD∥BC,∠B=45°,∠D=120°,AB=6cm,则DC的长为2$\sqrt{6}$cm.