题目内容
13.按要求解答下列问题(1)解不等式$\frac{2x-1}{3}$≤$\frac{3x+2}{4}$-1,并将解集在数轴上表示出来;
(2)解不等式组$\left\{\begin{array}{l}{4(x+1)≤7x+10}\\{x-5<\frac{x-8}{3}}\end{array}\right.$,并写出它所有的自然数解.
分析 (1)去分母、去括号、移项合并同类项,系数化成1即可求解;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:(1)去分母,得4(2x-1)≤3(3x+2)-12,
去括号,得8x-4≤9x+6-12,
移项,得8x-9x≤6-12+4,
合并同类项,得-x≤-2,
系数化成1得x≥2.
(2)$\left\{\begin{array}{l}{4(x+1)≤7x+10…①}\\{x-5<\frac{x-8}{3}…②}\end{array}\right.$,
解①得x≥-2,
解②得x<3.5
则不等式组的解集是-2≤x<3.5,则自然数解是:0,1,2,3.
点评 此题考查的是一元一次不等式和不等式组的解法,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
3.一个圆锥形的冰淇淋纸筒,其底面直径为6cm,母线长5cm,围成这样的冰淇淋纸筒所需纸片的面积是( )
| A. | 66πcm2 | B. | 15πcm2 | C. | 28πcm2 | D. | 30πcm2 |
18. 如图,BE=CF,AB=DE,添加下列哪些条件可以推证△ABC≌△DEF( )
如图,BE=CF,AB=DE,添加下列哪些条件可以推证△ABC≌△DEF( )
 如图,BE=CF,AB=DE,添加下列哪些条件可以推证△ABC≌△DEF( )
如图,BE=CF,AB=DE,添加下列哪些条件可以推证△ABC≌△DEF( )| A. | BC=EF | B. | ∠C=∠F | C. | AB∥DE | D. | ∠A=∠D |
 如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.
如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.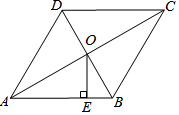 如图,菱形ABCD的对角线AC,BD相交于点O,且AC=16,BD=12.
如图,菱形ABCD的对角线AC,BD相交于点O,且AC=16,BD=12. 先在给定的数轴上画出下列各数所对应的点:-3,1.5,0,2$\frac{1}{2}$;再将这些数按照从小到大的顺序用“<”号连接起来.
先在给定的数轴上画出下列各数所对应的点:-3,1.5,0,2$\frac{1}{2}$;再将这些数按照从小到大的顺序用“<”号连接起来.