题目内容
2.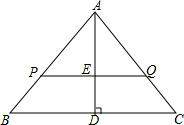 已知,在△ABC中,AB=AC=5,BC=6,PQ∥BC,AD⊥BC,与PQ交于E
已知,在△ABC中,AB=AC=5,BC=6,PQ∥BC,AD⊥BC,与PQ交于E(1)当S△PQA=SPBCQ时,求AE的长;
(2)当△PAQ的周长与四边形PBCQ的周长相等时,求AP的长度.
分析 (1)根据等腰三角形的性质得到BD=$\frac{1}{2}$BC=3,由勾股定理求得AD=4,由已知条件得到S△PQA=$\frac{1}{2}$S△ABC,通过△PQA∽△ABC,根据相似三角形的性质即可得到结论;
(2)根据已知条件推出AP+AQ=PB+6+CQ,由三角形相似得到△APQ是等腰三角形,于是得到AP=AQ=5-PB,设AP=AQ=x,列方程即可求得结论.
解答 解:(1)∵AB=AC,AD⊥BC,
∴BD=$\frac{1}{2}$BC=3,
∵AB=5,
∴AD=4,
∵S△PQA=SPBCQ,
∴S△PQA=$\frac{1}{2}$S△ABC,
∴$\frac{{S}_{△PQA}}{{S}_{△ABC}}$=$\frac{1}{2}$,
∵PQ∥BC,
∴△PQA∽△ABC,
∴$\frac{{S}_{△PQA}}{{S}_{△ABC}}$=($\frac{AE}{AD}$)2=$\frac{1}{2}$,
∴AE=2$\sqrt{2}$;
(2)∵△PAQ的周长与四边形PBCQ的周长相等,
∴AP+AQ+PO=PB+BC+CQ+PQ,
∴AP+AQ=PB+6+CQ,
∵△APQ∽△ABC,
∴△APQ是等腰三角形,
∴AP=AQ=5-PB,
设AP=AQ=x,
∴PB=QC=5-x,
∴2x=10-2x+6,
∴x=4,
∴AP=4.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
16.下列不属于分式$\frac{1}{2{x}^{2}-18}$与$\frac{x}{4x+12}$的公分母的是( )
| A. | (2x2-18)(4x+12) | B. | 16(x-3)(x+3) | C. | 4(x-3)(x+3) | D. | 2(x+3)(x-3) |
14.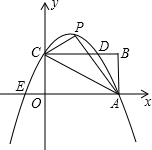 如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )
如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )
 如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )
如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )| A. | $\frac{7}{4}$$\sqrt{3}$ | B. | $\frac{7}{16}$$\sqrt{3}$ | C. | $\frac{7}{8}$$\sqrt{3}$ | D. | $\frac{7}{8}$ |
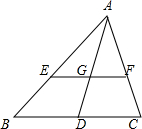 如图,在△ABC中,AD为BC边上的中线,EF∥BC,分别交AC于点E,F,交AD于点G,求证:EG=GF.
如图,在△ABC中,AD为BC边上的中线,EF∥BC,分别交AC于点E,F,交AD于点G,求证:EG=GF.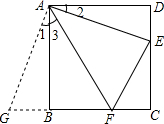 如图,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.
如图,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF. (1)计算:(-2)÷(-2÷$\frac{1}{2}$)-|-3|×(-1)+(-0.5)
(1)计算:(-2)÷(-2÷$\frac{1}{2}$)-|-3|×(-1)+(-0.5)