题目内容
17.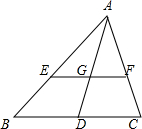 如图,在△ABC中,AD为BC边上的中线,EF∥BC,分别交AC于点E,F,交AD于点G,求证:EG=GF.
如图,在△ABC中,AD为BC边上的中线,EF∥BC,分别交AC于点E,F,交AD于点G,求证:EG=GF.
分析 根据已知条件得到△AEG∽△ABD,△AFG∽△ACD,推出$\frac{GE}{BD}=\frac{GF}{CD}$,根据BD=CD即可得到结论.
解答 证明:∵EF∥BC,
∴△AEG∽△ABD,△AFG∽△ACD,
∴$\frac{GE}{BD}=\frac{AG}{AD}$,$\frac{GF}{CD}=\frac{AG}{AD}$,
∴$\frac{GE}{BD}=\frac{GF}{CD}$,
∵AD为△ABC的边BC上的中线,
∴BD=CD,
∴GF=GE.
点评 本题考查了相似三角形的性质和判定,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
9.有一种长方体集装箱,其内空长为5米,高4.5米,宽3.4米,用这样的集装箱运长为5米,横截面的外圆直径为0.8米的圆柱形钢管,最多能运( )根.
| A. | 20根 | B. | 21根 | C. | 24根 | D. | 25根 |

 已知在△ABC中,AB=BC,D是BC的中点,CF∥AB,试说明BP2=PE•PF.
已知在△ABC中,AB=BC,D是BC的中点,CF∥AB,试说明BP2=PE•PF.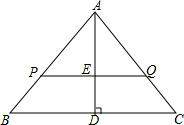 已知,在△ABC中,AB=AC=5,BC=6,PQ∥BC,AD⊥BC,与PQ交于E
已知,在△ABC中,AB=AC=5,BC=6,PQ∥BC,AD⊥BC,与PQ交于E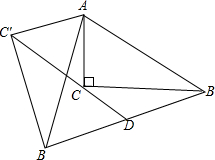 在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转,B、C旋转后的对应点分别是B′和C′.连接C′C并延长交B′B于点D.
在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转,B、C旋转后的对应点分别是B′和C′.连接C′C并延长交B′B于点D.