题目内容
14.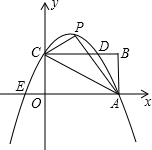 如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )
如图,矩形OABC的长OA=$\sqrt{3}$,宽OC=1,将△AOC沿AC翻折得△APC,经过C,P,A三点的抛物线与矩形OABC边CB相交于点D,则梯形COAD的面积为( )| A. | $\frac{7}{4}$$\sqrt{3}$ | B. | $\frac{7}{16}$$\sqrt{3}$ | C. | $\frac{7}{8}$$\sqrt{3}$ | D. | $\frac{7}{8}$ |
分析 根据矩形的边长求得点P的坐标,利用待定系数法求得抛物线的解析式,然后将D的纵坐标代入求出点D的横坐标,最后根据梯形的面积公式求解.
解答 解:∵OA=$\sqrt{3}$,OC=1,
∴tan∠OAC=$\frac{\sqrt{3}}{3}$,
∴∠OAC=30°,∠ACP=∠ACO=60°,
过P作PM⊥OA于M,交CB于G,
则PG⊥CD,
∠GCP=30°,GP=$\frac{1}{2}$CP=$\frac{1}{2}$OC=$\frac{1}{2}$,
CG=$\frac{\sqrt{3}}{2}$.
∴P($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),
设过 A、P、C三点抛物线解析式为y=ax2+bx+c.
∴c=1,
∴$\left\{\begin{array}{l}{\frac{3}{4}a+\frac{\sqrt{3}}{2}b+1=\frac{3}{2}}\\{3a+\sqrt{3}b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{4}{3}}\\{b=\sqrt{3}}\end{array}\right.$,
∴y=-$\frac{4}{3}$x2+$\sqrt{3}$x+1,
∵四边形OABC为矩形,
∴设点D坐标为(m,1),
则-$\frac{4}{3}$m2+$\sqrt{3}$m+1=1,
解得:m=$\frac{3\sqrt{3}}{4}$或m=0(舍去),
则梯形COAD的面积为:$\frac{1}{2}$($\frac{3\sqrt{3}}{4}$+$\sqrt{3}$)×1=$\frac{7\sqrt{3}}{8}$.
故选C.
点评 本题考查了二次函数的综合应用,涉及了矩形的性质、图形的翻折变换、二次函数解析式的确定、梯形的面积公式等知识,涉及的知识点较多,难度较大.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案| A. | 20根 | B. | 21根 | C. | 24根 | D. | 25根 |
| A. | 1.043×108人 | B. | 1.043×107人 | C. | 1.043×104人 | D. | 1043×105人 |
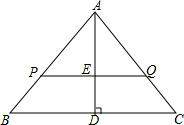 已知,在△ABC中,AB=AC=5,BC=6,PQ∥BC,AD⊥BC,与PQ交于E
已知,在△ABC中,AB=AC=5,BC=6,PQ∥BC,AD⊥BC,与PQ交于E
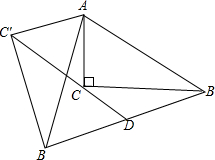 在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转,B、C旋转后的对应点分别是B′和C′.连接C′C并延长交B′B于点D.
在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转,B、C旋转后的对应点分别是B′和C′.连接C′C并延长交B′B于点D.