题目内容
7.设常数k是实数,(x1,y1)、(x2,y2)是关于x,y的方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{12}+\frac{{y}^{2}}{3}=1,①}\\{y=k(x+3),②}\end{array}\right.$的两个实数解.(1)若k=-1,求x1+x2的值;
(2)若x1+x2=-1,求k的值.
分析 (1)把k=-1代入方程②,得到方程③,把③代入①,得到关于x的一元二次方程,根据根与系数的关系计算即可;
(2)把②代入①得到关于x的一元二次方程,根据根与系数列式求出k的值.
解答 解:(1)当k=-1时,y=-x-3③,
把③代入①得,$\frac{{x}^{2}}{12}+\frac{(-x-3)^{2}}{3}=1$,
整理得,5x2+24x+24=0,
则x1+x2=-$\frac{24}{5}$;
(2)把②代入①得,$\frac{{x}^{2}}{12}+\frac{{k}^{2}(x+3)^{2}}{3}=1$,
整理得,(4k2+1)x2+24k2x+36k2-12=0,
x1+x2=-$\frac{24{k}^{2}}{4{k}^{2}+1}$-1,
解得,k=±$\frac{\sqrt{5}}{10}$.
点评 本题考查的是高次方程的解法,掌握代入消元法的一般步骤和一元二次方程根与系数的关系是解题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
17.下列各组二次根式,属于同类二次根式的是( )
| A. | $\sqrt{12}$与$\sqrt{72}$ | B. | $\sqrt{0.5}$与$\sqrt{\frac{2}{3}}$ | C. | $\sqrt{4{x}^{3}}$与-2$\sqrt{2x}$ | D. | $\sqrt{63}$与$\sqrt{28}$ |
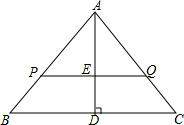 已知,在△ABC中,AB=AC=5,BC=6,PQ∥BC,AD⊥BC,与PQ交于E
已知,在△ABC中,AB=AC=5,BC=6,PQ∥BC,AD⊥BC,与PQ交于E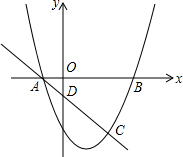 抛物线y=ax2+bx+c与x轴的交点为A(-1,0)和B(3,0),与直线y=-x+k相交于点A和点C(2,-3).
抛物线y=ax2+bx+c与x轴的交点为A(-1,0)和B(3,0),与直线y=-x+k相交于点A和点C(2,-3).