题目内容
9.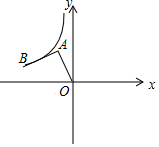 如图,在平面直角坐标系中,点A(-1,2),将AO绕点A顺时针旋转90°,点O的对应点B恰好落在双曲线y=$\frac{k}{x}$的图象上,则k的值为-3.
如图,在平面直角坐标系中,点A(-1,2),将AO绕点A顺时针旋转90°,点O的对应点B恰好落在双曲线y=$\frac{k}{x}$的图象上,则k的值为-3.
分析 作AC⊥y轴于C,AD⊥x轴,BD⊥y轴,它们相交于D,由A点坐标得到AC=1,OC=2,由于AO绕点A顺时针旋转90°,点O对应B点,所以相当是把△AOC绕点A顺时针旋转90°得到△ABD,根据旋转的性质得AD=AC=1,BD=OC=2,由此可得到B点坐标为(-3,1),然后根据反比例函数图象上点的坐标特征计算k的值.
解答  解:作AC⊥y轴于C,AD⊥x轴,BD⊥y轴,它们相交于D,如图,
解:作AC⊥y轴于C,AD⊥x轴,BD⊥y轴,它们相交于D,如图,
∵A点坐标为(-1,2),
∴AC=1,OC=2,
∵AO绕点A顺时针旋转90°,点O对应B点,
即把△AOC绕点A顺时针旋转90°得到△ABD,
∴AD=AC=1,BD=OC=2,
∴B点坐标为(-3,1),
∴k=-3×1=-3.
故答案为-3.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了坐标与图形变化-旋转.

练习册系列答案
相关题目
18.东岳中学初四年级进行了一次模拟考试,参加人数为1016人,为了了解这次考试的成绩情况,下列抽取样本合理的是( )
| A. | 抽取前100名学生的成绩 | B. | 抽取后100名学生的成绩 | ||
| C. | 抽取(1)(2)两个班的学生成绩 | D. | 抽取学号为4的倍数的学生的成绩 |
 如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M,若正方形ABCD的边长为2,则正方形DEFG的面积为$\frac{32}{9}$.
如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M,若正方形ABCD的边长为2,则正方形DEFG的面积为$\frac{32}{9}$.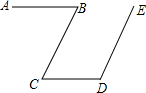 如图,已知AB∥CD,BC∥ED,请你猜想∠B与∠D之间具有什么数量关系,并说明理由.
如图,已知AB∥CD,BC∥ED,请你猜想∠B与∠D之间具有什么数量关系,并说明理由.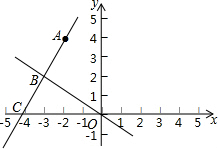 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-$\frac{2}{3}$x的图象交于点B(m,2)
如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-$\frac{2}{3}$x的图象交于点B(m,2)