题目内容
11.现要设计一个面积为100m2的养鸡场地,有两种设计方案:一种是设计成正方形场地,一种是设计成圆形场地,且不论采用哪种方案,养鸡场地的四周均要用竹篱笆围起来,试根据所学知识判断采用哪一种方案所要用的竹篱笆少?分析 根据正方形的面积公式可求正方形场地的边长,根据正方形的周长公式可求设计成正方形场地的竹篱笆长;根据圆的面积公式可求圆形场地的半径,根据圆的周长公式可求设计成圆形场地的竹篱笆长,再比较大小即可求解.
解答 解:$\sqrt{100}$=10(m),
10×4=40(m);
$\sqrt{\frac{100}{π}}$=$\frac{10}{π}$$\sqrt{π}$(m),
2π$\frac{10}{π}$$\sqrt{π}$=20$\sqrt{π}$(m),
∵40>20$\sqrt{π}$,
∴圆形场地所要用的竹篱笆少.
点评 考查了算术平方根,本题关键是求得正方形场地的边长,圆形场地的半径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.一个正数的算术根为m,则比这个数大2的数的算术平方根是( )
| A. | $\sqrt{{m}^{2}+2}$ | B. | $\sqrt{m+2}$ | C. | m2+2 | D. | m+2 |
16. 如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )
如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )
 如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )
如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )| A. | $({\sqrt{2}-1})a$ | B. | $\frac{{\sqrt{2}-1}}{2}a$ | C. | $\frac{{2-\sqrt{2}}}{4}a$ | D. | $({2-\sqrt{2}})a$ |
3. 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
20.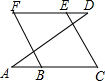 如图,能够判断FB∥CE的条件是( )
如图,能够判断FB∥CE的条件是( )
 如图,能够判断FB∥CE的条件是( )
如图,能够判断FB∥CE的条件是( )| A. | ∠F+∠C=180° | B. | ∠ABF=∠C | C. | ∠F=∠C | D. | ∠A=∠D |
1.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如表:
经检查,发现表格中恰好有一组数据计算错误,错误的那组数据的序号是( )
| 序号 | ① | ② | ③ | ④ | ⑤ |
| x | 0 | 1 | 2 | 3 | 4 |
| y | 8 | 3 | 0 | 1 | 0 |
| A. | ① | B. | ② | C. | ③ | D. | ④ |
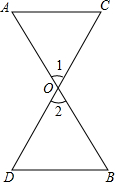 如图所示,AB,CD相交于点O,∠A=∠1,∠B=∠2,AC与BD平行吗?为什么?
如图所示,AB,CD相交于点O,∠A=∠1,∠B=∠2,AC与BD平行吗?为什么?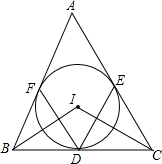 如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证:
如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证: