题目内容
16. 如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )
如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )| A. | $({\sqrt{2}-1})a$ | B. | $\frac{{\sqrt{2}-1}}{2}a$ | C. | $\frac{{2-\sqrt{2}}}{4}a$ | D. | $({2-\sqrt{2}})a$ |
分析 本题已知正方形的对角线长是a,就可求出正方形的边长,从而求解.
解答 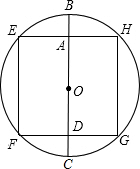 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:
对角线长为a的正方形桌面的边长EF=$\frac{\sqrt{2}}{2}$a,
又∵四边形AEFD为矩形,
∴AD=EF=$\frac{\sqrt{2}}{2}$a,又BC=a,
∴AB=$\frac{BC-AD}{2}$=$\frac{a-\frac{\sqrt{2}}{2}a}{2}=\frac{2-\sqrt{2}}{4}a$,
则桌布下垂的最大长度为$\frac{2-\sqrt{2}}{4}a$.
故选C.
点评 本题考查垂径定理的应用,关键是利用了圆内接正方形的边长与圆的直径的关系求解.

练习册系列答案
相关题目
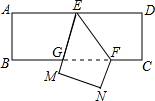 如图所示,把一张长方形纸片ABCD沿EF折叠,若∠AEG=60°,则∠EFG的度数是60°,则∠GFN度数是60°.
如图所示,把一张长方形纸片ABCD沿EF折叠,若∠AEG=60°,则∠EFG的度数是60°,则∠GFN度数是60°.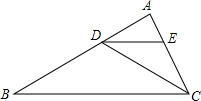 如图,已知∠ABC=30°,∠ADC=60°,DE为∠ADC的平分线,你能判断哪两条直线平行吗,并说明理由.
如图,已知∠ABC=30°,∠ADC=60°,DE为∠ADC的平分线,你能判断哪两条直线平行吗,并说明理由.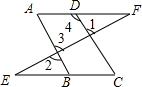 如图,已知∠1=∠2,∠A=∠C,证明:AF∥EC.
如图,已知∠1=∠2,∠A=∠C,证明:AF∥EC.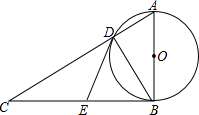 如图,在⊙O中,AB为直径,BC为⊙O的切线,D为⊙O上一点,AD的延长线与切线BC交于点C,E是BC的中点,连接DE,BD.
如图,在⊙O中,AB为直径,BC为⊙O的切线,D为⊙O上一点,AD的延长线与切线BC交于点C,E是BC的中点,连接DE,BD.