题目内容

抛物线y=ax2+bx+c经过点A（-1，2），B（1，-2），则a+c的值为（　　）
A、-2B、0C、2D、4
考点：二次函数图象上点的坐标特征
专题：计算题
分析：根据二次函数图象上点的坐标特征，把点A和点B的坐标分别代入解析式得到a-b+c=2，a+b+c=-2，然后把两式相加即可得到a+c的值．
解答：解：∵点A（-1，2），B（1，-2）在抛物线y=ax2+bx+c上，
∴a-b+c=2，a+b+c=-2，
二次函数图象上点的坐标特征∴2a+2c=0，
∴a+c=0．
故选B．
点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
练习册系列答案
相关题目
观察算式：
1
1×2
=1-
1
2
=
1
2
； 
1
1×2
+
1
2×3
=1-
1
2
+
1
2
-
1
3
=
2
3
1
1×2
+
1
2×3
+
1
3×4
=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
=
3
4

（1）按规律填空
1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
+…+
1
99×100
=
 
；
（2）如果有理数a，b满足|ab-2|+（1-b）2=0，
1
ab
+
1
(a+1)(b+1)
+
1
(a+2)(b+2)
+…+
1
(a+2004)(b+2004)
的值．
将直线y=-3x-2向下平移3个单位长度后得到的直线解析式是
 
．
如图，△ABC中，∠B的平分线与∠C的外角的平分线交于P点，PD⊥AC于D，PH⊥BA于H，
（1）若点P到直线BA的距离是5cm，求点P到直线BC的距离；
（2）求证：点P在∠HAC的平分线上．
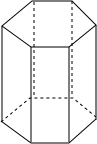如图，是一个正六棱柱，它的底面边长是3cm，高是6cm．
（1）这个棱柱的侧面积是多少？
（2）这个棱柱共有多少条棱？所有的棱长的和是多少？
（3）这个棱柱共有多少个顶点？
（4）通过观察，试用含n的式子表示n棱柱的面数与棱的条数．
已知y关于x的反比例函数y=
m-5
x
（m为常数）经过点A（2，-1），求反比例函数的解析式．
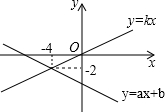如图，已知一次函数y=ax+b（a≠0）和y=kx（k≠0）的图象交于点P，则一元一次不等式ax+b≤kx的解集是
 
．
解方程：
（1）2x2-3x-2=0；                 
（2）2x2-3x-1=0．（用配方法）
先化简，再求值：
2（a2-a-1）-（a2-a-1）+3（a2-a-1），其中a=-
1
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网