题目内容
 如图,△ABC中,∠B的平分线与∠C的外角的平分线交于P点,PD⊥AC于D,PH⊥BA于H,
如图,△ABC中,∠B的平分线与∠C的外角的平分线交于P点,PD⊥AC于D,PH⊥BA于H,(1)若点P到直线BA的距离是5cm,求点P到直线BC的距离;
(2)求证:点P在∠HAC的平分线上.
考点:角平分线的性质
专题:证明题
分析:(1)过P作PF⊥BE于F,由于BP平分∠ABC,PH⊥BA,PF⊥BE,则根据角平分线的性质即可得到PH=PF=5cm;
(2)根据角平分线的性质得PF=PD,则PD=PH,于是根据到角的两边距离相等的点在这个角的平分线上得到AP平分∠HAD.
(2)根据角平分线的性质得PF=PD,则PD=PH,于是根据到角的两边距离相等的点在这个角的平分线上得到AP平分∠HAD.
解答: (1)解:过P作PF⊥BE于F,如图,
(1)解:过P作PF⊥BE于F,如图,
∵BP平分∠ABC,PH⊥BA于H,PF⊥BE于F,
∴PH=PF=5cm,
∴点P到直线BC的距离为5cm;
(2)证明:∵CP平分∠ACE,PD⊥AC于D,PF⊥BE于F,
∴PF=PD,
∴PD=PH,
∴AP平分∠HAD.
 (1)解:过P作PF⊥BE于F,如图,
(1)解:过P作PF⊥BE于F,如图,∵BP平分∠ABC,PH⊥BA于H,PF⊥BE于F,
∴PH=PF=5cm,
∴点P到直线BC的距离为5cm;
(2)证明:∵CP平分∠ACE,PD⊥AC于D,PF⊥BE于F,
∴PF=PD,
∴PD=PH,
∴AP平分∠HAD.
点评:本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了角平分线定理的逆定理.

练习册系列答案
相关题目
小明沿着坡度为1:
的山坡向上走了1 000m,则他升高了( )
| 3 |
A、200
| ||
| B、500m | ||
C、500
| ||
| D、1 000m |
抛物线y=ax2+bx+c经过点A(-1,2),B(1,-2),则a+c的值为( )
| A、-2 | B、0 | C、2 | D、4 |
 △ABC内接于⊙O,AH⊥BC,垂足为H,AD平分∠BAC,交⊙O于点D.求证:AD平分∠HAO.
△ABC内接于⊙O,AH⊥BC,垂足为H,AD平分∠BAC,交⊙O于点D.求证:AD平分∠HAO.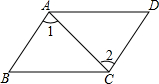 如图,AB∥CD,AB=CD.问:△ABC和△CDA是全等三角形吗?为什么?
如图,AB∥CD,AB=CD.问:△ABC和△CDA是全等三角形吗?为什么?