题目内容
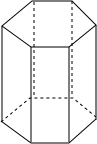 如图,是一个正六棱柱,它的底面边长是3cm,高是6cm.
如图,是一个正六棱柱,它的底面边长是3cm,高是6cm.(1)这个棱柱的侧面积是多少?
(2)这个棱柱共有多少条棱?所有的棱长的和是多少?
(3)这个棱柱共有多少个顶点?
(4)通过观察,试用含n的式子表示n棱柱的面数与棱的条数.
考点:认识立体图形,欧拉公式
专题:
分析:(1)根据底面边长乘以高,可得一个侧面的面积,根据一个侧面的面积乘以6,可得答案;
(2)根据六棱柱的特点,可得棱的条数,根据有理数的加法,可得棱长的和;
(3)根据三条棱交于一点,可得棱柱的顶点;
(4)根据几棱柱有几个侧面,棱柱都有两个底面,可得棱柱的面,根据几棱柱有几条侧棱,底面的棱是几的二倍,可得棱的条数.
(2)根据六棱柱的特点,可得棱的条数,根据有理数的加法,可得棱长的和;
(3)根据三条棱交于一点,可得棱柱的顶点;
(4)根据几棱柱有几个侧面,棱柱都有两个底面,可得棱柱的面,根据几棱柱有几条侧棱,底面的棱是几的二倍,可得棱的条数.
解答:解:(1)正六棱柱的侧面积3×6×6=108(cm2);
(2)这个棱柱共有 6+6+6=18条棱;
所有的棱长的和是12×3+6×6=36+36=72(cm);
(3)这个棱柱共有12个顶点;
(4)n棱柱的面数是(n+2)面,
n棱柱棱的条数是3n条.
(2)这个棱柱共有 6+6+6=18条棱;
所有的棱长的和是12×3+6×6=36+36=72(cm);
(3)这个棱柱共有12个顶点;
(4)n棱柱的面数是(n+2)面,
n棱柱棱的条数是3n条.
点评:本题考查了认识立体图形,n棱柱的面是(n+2)个,棱是3n条,顶点是2n个.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
A为数轴上表示2的点,将点A沿数轴向左平移7个单位到点B,再由B向右平移6个单位到点C,则点C所表示的数是( )
| A、11 | B、1 | C、2 | D、3 |
抛物线y=ax2+bx+c经过点A(-1,2),B(1,-2),则a+c的值为( )
| A、-2 | B、0 | C、2 | D、4 |
在△ABC的三个顶点A(2,-3),B(-4,-5),C(-3,2)中,可能在反比例函数y=
(k>0)的图象上的点是( )
| k |
| x |
| A、点A | B、点B |
| C、点C | D、三个点都在 |
 如图所示,已知:AB是⊙O的直径,CB是⊙O的弦,过点B作BD⊥CP于D,若CP是⊙O的切线.
如图所示,已知:AB是⊙O的直径,CB是⊙O的弦,过点B作BD⊥CP于D,若CP是⊙O的切线. △ABC内接于⊙O,AH⊥BC,垂足为H,AD平分∠BAC,交⊙O于点D.求证:AD平分∠HAO.
△ABC内接于⊙O,AH⊥BC,垂足为H,AD平分∠BAC,交⊙O于点D.求证:AD平分∠HAO.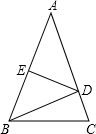 如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.
如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.