题目内容
2.下列说法正确的是( )①内错角相等;②过直线外一点有且只有一条直线与已知直线平行;③相等的角是对顶角;④幂的乘方,底数不变,指数相加;⑤两个角的和为90°,则这两个角互补.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分别利用平行公理以及幂的乘方运算法则、互余的定义、对顶角的定义分别分析得出答案.
解答 解:①两直线平行,内错角相等,故此选项错误;
②过直线外一点有且只有一条直线与已知直线平行,正确;
③相等的角不一定是对顶角,故此选项错误;
④幂的乘方,底数不变,指数相乘,故此选项错误;
⑤两个角的和为90°,则这两个角互余,故此选项错误,
故选:A.
点评 此题主要考查了平行公理以及幂的乘方运算、互余的定义、对顶角的定义等知识,正确把握相关定义是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.研究发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间有如下关系:(0≤x≤30)
根据以上信息,回答下列问题:
(1)表中描述的变化过程中,自变量是什么?因变量是什么?
(2)当提出概念所用的时间为10分钟时,学生的接受能力约是多少?
(3)当提出概念所用的时间为多少分钟时,学生的接受能力最强?
(4)在什么时间范围内,学生的接受能力在逐渐增强?什么时间范围内,学生的接受能力在逐渐增强减弱?
| 提出概念所用的时间x(分钟) | 2 | 5 | 7 | 10 | 12 | 13 | 14 | 17 | 20 |
| 对概念的接受能力y | 47.8 | 53.5 | 56.3 | 59 | 59.8 | 59.9 | 59.8 | 58.3 | 55 |
(1)表中描述的变化过程中,自变量是什么?因变量是什么?
(2)当提出概念所用的时间为10分钟时,学生的接受能力约是多少?
(3)当提出概念所用的时间为多少分钟时,学生的接受能力最强?
(4)在什么时间范围内,学生的接受能力在逐渐增强?什么时间范围内,学生的接受能力在逐渐增强减弱?
7.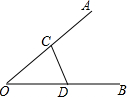 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )| A. | 线段CD的中点 | B. | CD与∠AOB平分线的交点 | ||
| C. | OC垂直平分线与CD的交点 | D. | OD垂直平分线与CD的交点 |
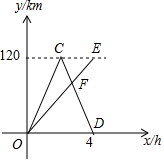 A,B两地相距120km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即按原速返回.如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象.
A,B两地相距120km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即按原速返回.如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象. 如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2=50°.
如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2=50°.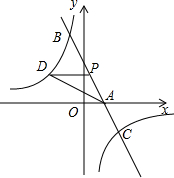 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点.点P(m,n)是一次函数y1=kx+b的图象上的动点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点.点P(m,n)是一次函数y1=kx+b的图象上的动点.