题目内容
16.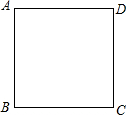 在正方形ABCD中,点E是边BC上的中点,在边CD上取一点F,使得AE平分∠BAF.
在正方形ABCD中,点E是边BC上的中点,在边CD上取一点F,使得AE平分∠BAF.(1)依题意补充图形;
(2)小玲画图结束后,通过观察、测量,提出猜想:线段AF等于线段BC与线段CF的和.小玲把这个猜想与同学们进行交流.通过讨论,形成了证明该猜想的几种想法:
想法1:考虑到AE平分∠BAF,且∠B=90°.若过点E作EM⊥AF,则易证AM=AB=BC.这样,只需证明FM=FC即可.因∠EMF=∠C=90°,证FM=FC即证EF平分∠MEC,所以连接EF.
想法2:考虑到E是BC中点,若延长AE,交DC的延长线于点G,则易证CG=AB,则CF+BC=CF+CG=FG.要证AF=BC+CF,只需证FA=FG即可.
想法3:小米在课外小组学习了梯形中位线的相关知识,考虑到正方形ABCD所以有BC=AB,因此BC+CF=AB+CF,是梯形上、下底之和,结合“E是BC中点”,易联想到梯形中位线的性质,从而解决问题.
…
请你参考上面的想法,帮助小玲证明AF=BC+CF.(一种方法即可)
分析 (1)根据题意作出图形即可;
(2)想法1:作EM⊥AF于M,连接EF,根据已知和正方形的性质分别证明Rt△ABE≌Rt△AMERt,Rt△EMF≌Rt△ECF,得出EM=BE,FM=FC,从而得出结论;
想法2:如图3,延长AE、DC交于点G,根据全等三角形的性质得到AB=CG,∠1=∠G,由角平分线的性质得到∠1=∠2,等量代换得到∠2=∠G于是得到结论;
想法3:过中点E作EM∥AB,交AF于M.通过中位线的性质证明EM=$\frac{1}{2}$(AB+CF),从而得出结论.
解答  解:(1)补充图形,如图1所示;
解:(1)补充图形,如图1所示;
想法1:如图2,作EM⊥AF于M.
∵∠B=90°,
∴∠B=∠AME=90°,
∵∠1=∠2,
∴BE=EM,
在Rt△ABE与Rt△AME中,$\left\{\begin{array}{l}{BE=EM}\\{AE=AE}\end{array}\right.$,
∴Rt△ABE≌Rt△AME.
∴AM=AB=BC,EM=BE.①
连接EF,E是BC中点,
∴EC=BE=EM
在Rt△AEMF与Rt△ECF中$\left\{\begin{array}{l}{EM=EC}\\{EF=EF}\end{array}\right.$,
∴Rt△EMF≌Rt△ECF,
∴FM=FC、②
综合①、②得AF=AM+MF=BC+CF.
想法2:如图3,延长AE、DC交于点G,
∵E是BC中点,
∴BE=CE,
∵∠B=∠GCE,∠AEB=∠GEC,在△AEB与△GEC中,$\left\{\begin{array}{l}{∠B=∠GEC}\\{BE=CE}\\{∠AEB=∠GEC}\end{array}\right.$,
∴△AEB≌△GEC,
∴AB=CG,∠1=∠G,
∵AE平分∠BAF,
∴∠1=∠2,
∴∠2=∠G
∴AF=FG=FC+CG,
∴AF=BC+CF;
想法3:如图4,过中点E作EM∥AB,交AF于M.则AM=MF,且∠1=∠2=∠3.
∴EM=AM=$\frac{1}{2}$AF
∵EM=$\frac{1}{2}$(AB+CF),
∴AF=AB+CF=BC+CF.
点评 本题考查了正方形的性质,及全等三角形的判定和性质.合理的将AF分成与BC,CF相等的两份是解题的关键,本题难度较大.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案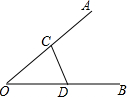 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )| A. | 线段CD的中点 | B. | CD与∠AOB平分线的交点 | ||
| C. | OC垂直平分线与CD的交点 | D. | OD垂直平分线与CD的交点 |
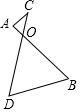 如图,AB=CD,AB与DC相交于点O,∠AOC=60°,请你利用平移的有关知识说明:AC+BD>AB.
如图,AB=CD,AB与DC相交于点O,∠AOC=60°,请你利用平移的有关知识说明:AC+BD>AB.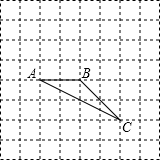 如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上. 如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2=50°.
如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2=50°. 如图,点E为正方形ABCD内一点,连接AE,BE,CE,∠AEB=90°,若AE=2,BE=3,则CE=$\sqrt{10}$.
如图,点E为正方形ABCD内一点,连接AE,BE,CE,∠AEB=90°,若AE=2,BE=3,则CE=$\sqrt{10}$. 如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2.
如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2. (1)已知x+y=4,x2+y2=9,求xy的值;
(1)已知x+y=4,x2+y2=9,求xy的值;