题目内容
19.【知识链接】(1)有理化因式:两个含有根式的代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:$\sqrt{2}$的有理化因式是$\sqrt{2}$;1-$\sqrt{{x}^{2}+2}$的有理化因式是1+$\sqrt{{x}^{2}+2}$.
(2)分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去,指的是如果二次根式中分母有根号,那么通常在分子、分母上同乘以一个二次根式,达到化去分母中根号的目的.
【知识运用】
(1)填空:2$\sqrt{x}$的有理化因式是$\sqrt{x}$;a+$\sqrt{b}$的有理化因式是a-$\sqrt{b}$;-$\sqrt{m-1}$-$\sqrt{m+1}$的有理化因式是$-\sqrt{m-1}+\sqrt{m+1}$.
(2)把下列各式的分母有理化:
①$\frac{1}{x+\sqrt{y}}$;②$\frac{\sqrt{6}+\sqrt{2}}{\sqrt{2}-\sqrt{6}}$.
分析 (1)根据题意即可求出有理化因式;
(2)根据题意即可进行分母有理化;
解答 解:(1)$\sqrt{x}$;a-$\sqrt{b}$;$-\sqrt{m-1}$+$\sqrt{m+1}$
(2)①$\frac{1}{x+\sqrt{y}}$=$\frac{x-\sqrt{y}}{(x+\sqrt{y})(x-\sqrt{y})}$=$\frac{x-\sqrt{y}}{{x}^{2}-y}$
②$\frac{\sqrt{6}+\sqrt{2}}{\sqrt{2}-\sqrt{6}}$=$\frac{(\sqrt{6}+\sqrt{2})^{2}}{(\sqrt{2}-\sqrt{6})(\sqrt{2}+\sqrt{6})}$=$\frac{6+4\sqrt{3}+2}{2-6}$=-2-$\sqrt{3}$
故答案为:(1)$\sqrt{x}$;a-$\sqrt{b}$;$-\sqrt{m-1}$+$\sqrt{m+1}$
点评 本题考查分母有理化,解题的关键是正确理解题意,本题属于基础题型.

练习册系列答案
相关题目
7.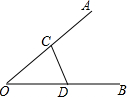 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )| A. | 线段CD的中点 | B. | CD与∠AOB平分线的交点 | ||
| C. | OC垂直平分线与CD的交点 | D. | OD垂直平分线与CD的交点 |
 如图所示,A、B的坐标分别为(2,0),(0,1),AB∥A1B1,AB=A1B1,则a-b的值是( )
如图所示,A、B的坐标分别为(2,0),(0,1),AB∥A1B1,AB=A1B1,则a-b的值是( )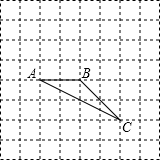 如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上. 如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2=50°.
如图,将一个长方形条折成如图所示的形状,若已知∠1=100°,则∠2=50°.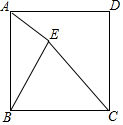 如图,点E为正方形ABCD内一点,连接AE,BE,CE,∠AEB=90°,若AE=2,BE=3,则CE=$\sqrt{10}$.
如图,点E为正方形ABCD内一点,连接AE,BE,CE,∠AEB=90°,若AE=2,BE=3,则CE=$\sqrt{10}$.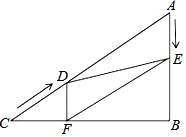 如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿
如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿