题目内容
4.下列运算正确的是( )| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$×$3\sqrt{3}$=6$\sqrt{3}$ | C. | $\sqrt{2}$$÷\sqrt{3}$=$\frac{\sqrt{6}}{3}$ | D. | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ |
分析 根据二次根式的加减法对A、D进行判断;根据二次根式的乘法法则对B进行判断;根据二次根式的除法法则对C进行判断.
解答 解:A、$\sqrt{2}$与$\sqrt{3}$不能合并,所以A选项计算错误;
B、原式=6×3=18,所以B选项计算错误;
C、原式=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,所以C选项计算正确;
D、5$\sqrt{5}$与2$\sqrt{2}$不能合并,所以D选项计算错误.
故选C.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
12.已知A(1,y1),B(-2,y2)两点在双曲线y=$\frac{m}{x}$上,且y2>y1,则m的取值范围是( )
| A. | m<0 | B. | m>0 | C. | m≥0 | D. | m≤0 |
19.若把分式$\frac{2xy}{x+y}$(x,y为正数)中的x,y分别扩大为原来的2倍,则分式的值是( )
| A. | 扩大为原来的2倍 | B. | 缩小为原来的2倍 | C. | 扩大为原来的4倍 | D. | 不变 |
9.在平面直角坐标系xoy中,对于点P(x,y),我们把点p′(-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为( )
| A. | (-3,3) | B. | (-2,-2) | C. | (3,-1) | D. | (2,4) |
16. 如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC≌△DAE的是( )
如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC≌△DAE的是( )
 如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC≌△DAE的是( )
如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC≌△DAE的是( )| A. | AC=AE | B. | BC=DE | C. | ∠B=∠D | D. | ∠C=∠E |
14.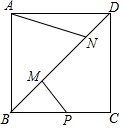 如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )
如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )
 如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )
如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 6 | D. | 3$\sqrt{5}$ |
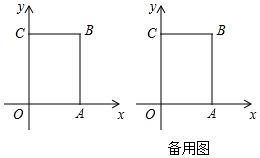 如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a,b满足|a-4|+$\sqrt{b-6}$=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a,b满足|a-4|+$\sqrt{b-6}$=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.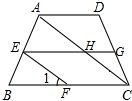 如图,AD∥EG∥BC,AC∥EF,若∠1=50°,则∠AHG=130°.
如图,AD∥EG∥BC,AC∥EF,若∠1=50°,则∠AHG=130°. 如图,将周长为16的三角形ABC沿BC方向平移3个单位得到三角形DEF,则四边形ABFD的周长等于22.
如图,将周长为16的三角形ABC沿BC方向平移3个单位得到三角形DEF,则四边形ABFD的周长等于22.